Cosine and Sine Transforms

Please tell us how to improve our documentation:

Thank you for your feedback! If you want to participate in content improvement and share additional information, please click Feedback button.

Rate this document:

Language:

Input to the DFT that possess special symmetries occur in various applications. A transform that exploits symmetry usually saves in storage and computational count, such as with the real-to-complex and complex-to-real FFT transforms. The Performance Library cosine and sine transforms are special cases of FFT routines that take advantage of the symmetry properties found in even and odd functions.

Note - Oracle Developer Studio Performance Library sine and cosine transform routines are based on the routines contained in FFTPACK (http://www.netlib.org/fftpack/). Routines with a V prefix are vectorized routines that are based on the routines contained in VFFTPACK (http://www.netlib.org/vfftpack/).

Fast Cosine and Sine Transform Routines

The following tables list the Oracle Developer Studio Performance Library fast cosine and sine transforms. Names of double precision routines are in square brackets. Routines whose name begins with 'V' can compute the transform of one or more sequences simultaneously. Those whose name ends with 'I' are initialization routines.

Table 15 Fast Cosine Transforms for Even Sequences Routines and Their Arguments

Routine Name	Arguments
`COST` `[DCOST]`	`(LEN+1`, `X,` `WORK)`
`COSTI` `[DCOSTI]`	`(LEN+1,` `WORK)`
`VCOST` `[VDCOST]`	`(M,` `LEN+1,` `X,` `WORK,` `LD,` `TABLE)`
`VCOSTI` `[VDCOSTI]`	`(LEN+1,` `TABLE)`

Table 16 Fast Cosine Transforms for Quarter-Wave Even Sequences Routines and Their Arguments

Routine Name	Arguments
`COSQF` `[DCOSQF]`	`(LEN,` `X,` `WORK)`
`COSQB` `[DCOSQB]`	`(LEN,` `X,` `WORK)`
`COSQI` `[DCOSQI]`	`(LEN,` `WORK)`
`VCOSQF` `[VDCOSQF]`	`(M,` `LEN,` `X,` `WORK,` `LD,` `TABLE)`
`VCOSQB` `[VDCOSQB]`	`(M,` `LEN,` `X,` `WORK,` `LD,` `TABLE)`
`VCOSQI` `[VDCOSQI]`	`(LEN,` `TABLE)`

Table 17 Fast Sine Transforms for Odd Sequences Routines and Their Arguments

Routine Name	Arguments
`SINT` `[DSINT]`	`(LEN-1,` `X,` `WORK)`
`SINTI` `[DSINTI]`	`(LEN-1,` `WORK)`
`VSINT` `[VDSINT]`	`(M,` `LEN-1,` `X,` `WORK,` `LD,` `TABLE)`
`VSINTI` `[VDSINTI]`	`(LEN-1,` `TABLE)`

Table 18 Fast Sine Transforms for Quarter-Wave Odd Sequences Routines and Their Arguments

Routine Name	Arguments
`SINQF` `[DSINQF]`	`(LEN,` `X,` `WORK)`
`SINQB` `[DSINQB]`	`(LEN,` `X,` `WORK)`
`SINQI` `[DSINQI]`	`(LEN,` `WORK)`
`VSINQF` `[VDSINQF]`	`(M,` `LEN,` `X,` `WORK,` `LD,` `TABLE)`
`VSINQB` `[VDSINQB]`	`(M,` `LEN,` `X,` `WORK,` `LD,` `TABLE)`
`VSINQI` `[VDSINQI]`	`(LEN,` `TABLE)` Notes:

Note - Note the following information about the previous tables:

M: Number of sequences to be transformed.
LEN, LEN-1, LEN+1: Length of the input sequence or sequences.
X: A real array which contains the sequence or sequences to be transformed. On output, the real transform results are stored in X.
TABLE: Array of constants particular to a transform size that is required by the transform routine. The constants are computed by the initialization routine.
WORK: Workspace required by the transform routine. In routines that operate on a single sequence, WORK also contains constants computed by the initialization routine.

Fast Sine Transforms

Another type of symmetry that is commonly encountered is the odd symmetry where x(n) = -x(-n) for n = -N+1, …, 0, …, N. As in the case of the fast cosine transform, the fast sine transform (FST) takes advantage of the odd symmetry to save memory and computation. For a real odd sequence x, symmetry implies that x(0) = -x(0) = 0. Therefore, if x is of length 2N then only N = 1 values of x are required to compute the FST. Routine SINT computes the FST of a single real odd sequence while VSINT computes the FST of one or more sequences. Before calling [V]SINT, [V]SINTI must be called to compute trigonometric constants and factors associated with input length N-1. The FST is its own inverse transform. Calling VSINT twice will result in the original N -1 data points. Calling SINT twice will result in the original N-1 data points multiplied by 2N.

An odd sequence with symmetry such that x(n) = -x(-n - 1), where -N+1, …, 0, …, N is said to have quarter-wave odd symmetry. SINQF and SINQB compute the FST and its inverse, respectively, of a single real quarter-wave odd sequence while VSINQF and VSINQB operate on one or more sequences. SINQB is unnormalized, so using the results of SINQF as input in SINQB produces the original sequence scaled by a factor of 4N. However, VSINQB is normalized, so a call to VSINQF followed by a call to VSINQB will produce the original sequence. An FST of a real sequence of length 2N that has quarter-wave odd symmetry requires N input data points and produces an N-point resulting sequence. Initialization is required before calling the transform routines by calling [V]SINQI.

Fast Cosine Transforms

A special form of the FFT that operates on real even sequences is the fast cosine transform (FCT). A real sequence x is said to have even symmetry if x(n) = x(-n) where n = -N + 1, …, 0, …, N. An FCT of a sequence of length 2N requires N + 1 input data points and produces a sequence of size N + 1. Routine COST computes the FCT of a single real even sequence while VCOST computes the FCT of one or more sequences. Before calling [V]COST, [V]COSTI must be called to compute trigonometric constants and factors associated with input length N + 1. The FCT is its own inverse transform. Calling VCOST twice will result in the original N +1 data points. Calling COST twice will result in the original N +1 data points multiplied by 2N.

An even sequence x with symmetry such that x(n) = x(-n - 1) where n = ‐N + 1, … , 0, …, N is said to have quarter-wave even symmetry. COSQF and COSQB compute the FCT and its inverse, respectively, of a single real quarter-wave even sequence. VCOSQF and VCOSQB operate on one or more sequences. The results of [V]COSQB are unnormalized, and if scaled by 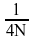image:1 over 4N the original sequences are obtained. An FCT of a real sequence of length 2N that has quarter-wave even symmetry requires N input data points and produces an N-point resulting sequence. Initialization is required before calling the transform routines by calling [V]COSQI.

Discrete Fast Cosine and Sine Transforms and Their Inverse

Oracle Developer Studio Performance Library routines use the equations in the following sections to compute the fast cosine and sine transforms and inverse transforms.

`[D]COST`: Forward and Inverse Fast Cosine Transform (FCT) of a Sequence

The forward and inverse FCT of a sequence is computed as:

image:X(k) = x(0) + 2 times sum to {N-1} from {n=1} x(n) cos((%pi nk) over N) + x(N) cos(%pi k), k=0,...,N

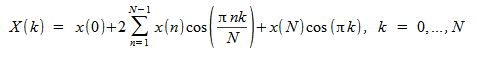
[D]COST Notes:

N + 1 values are needed to compute the FCT of an N-point sequence.
[D]COST also computes the inverse transform. When [D]COST is called twice, the result will be the original sequence scaled by

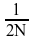
`V[D]COST`: Forward and Inverse Fast Cosine Transforms of Multiple Sequences (VFCT)

The forward and inverse FCTs of multiple sequences are computed as:

For i = 0, M - 1

image:X(i,k) = {x(i,0)}over 2N + 1 over N sum to {N - 1} from {n=1} x(i,n) cos ({%pi nk} over N ) + x(i,N) over 2N cos(%pi k), k= 0, ..., N1 .

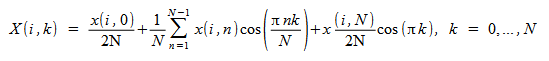V[D]COST Notes

M × (N+1) values are needed to compute the VFCT of M N-point sequences.
The input and output sequences are stored row-wise.
V[D]COST is normalized and is its own inverse. When V[D]COST is called twice, the result will be the original data.

`[D]COSQF`: Forward FCT of a Quarter-Wave Even Sequence

The forward FCT of a quarter-wave even sequence is computed as:

image:X(k)= x(0)+ 2 sum to {N - 1} from {n = 1} x(n) cos({%pi (2k+1)} over 2N), k= 0, ..., N - 1

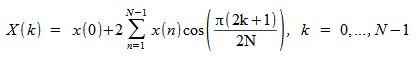
N values are needed to compute the forward FCT of an N-point quarter-wave even sequence.

`[D]COSQB`: Inverse FCT of a Quarter-Wave Even Sequence

The inverse FCT of a quarter-wave even sequence is computed as

image:x(n) = sum to {N - 1} from {k = 0} X(k) cos ({%pi n(2k + 1)} over 2N ), n = 0,...,N - 1 .

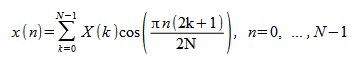Calling the forward and inverse routines will result in the original input scaled by 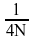image:1 over 4N .

`V[D]COSQF`: Forward FCT of One or More Quarter-Wave Even Sequences

The forward FCT of one or more quarter-wave even sequences is computed as

For i = 0, M - 1

image:X(i,k) = 1 over N [ x(i,0)+ 2 sum to {N - 1} from {n = 1} x(i,n) cos ({%pi n(2k + 1)} over 2N )], k = 0, ..., N - 1

V[D]COSQF Notes:

The input and output sequences are stored row-wise.
The transform is normalized so that if the inverse routine V[D]COSQB is called immediately after calling V[D]COSQF, the original data is obtained.

`V[D]COSQB`: Inverse FCT of One or More Quarter-Wave Even Sequences

The inverse FCT of one or more quarter-wave even sequences is computed as

For i = 0, M - 1

image:x(i,n) = sum to {N - 1} from {k = 0} X(i,k) cos ({%pi n(2k + 1)} over 2N), n = 0,...,N - 1

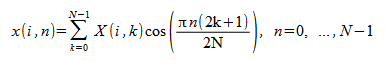
V[D]COSQB Notes:

The input and output sequences are stored row-wise.
The transform is normalized so that if V[D]COSQB is called immediately after calling V[D]COSQF, the original data is obtained.

`[D]SINT`: Forward and Inverse Fast Sine Transform (FST) of a Sequence

The forward and inverse FST of a sequence is computed as

image:X(k) = 2 times sum to {N - 2} from {n = 0} x(n) sin ({%pi (n+1)(k+1)} over N), k = 0,...,N - 2 .

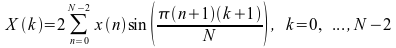[D]SINT Notes:

N-1 values are needed to compute the FST of an N-point sequence.
[D]SINT also computes the inverse transform. When [D]SINT is called twice, the result will be the original sequence scaled by .

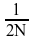`V[D]SINT`: Forward and Inverse Fast Sine Transforms of Multiple Sequences (VFST)

The forward and inverse fast sine transforms of multiple sequences are computed as

For i = 0, M - 1

image:X(i,k) = (2 over sqrt 2N) times sum to {N - 2} from {n = 0} x(i,n) sin ({%pi (n+1)(k+1)} over N), k = 0,...,N - 2 .

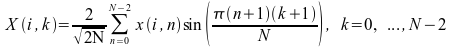V[D]SINT Notes:

M × (N - 1) values are needed to compute the VFST of M N-point sequences.
The input and output sequences are stored row-wise.
V[D]SINT is normalized and is its own inverse. Calling V[D]SINT twice yields the original data.

`[D]SINQF`: Forward FST of a Quarter-Wave Odd Sequence

The forward FST of a quarter-wave odd sequence is computed as

image:X(k) = 2 times sum to {N - 2} from {n = 0} x(n) sin ({%pi (n+1)(2k+1)} over 2N ) + x(N - 1) cos(%pi k), k = 0,...,N - 1 .

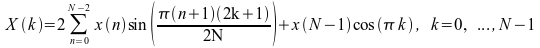N values are needed to compute the forward FST of an N-point quarter-wave odd sequence.

`[D]SINQB`: Inverse FST of a Quarter-Wave Odd Sequence

The inverse FST of a quarter-wave odd sequence is computed as

image:x(n) = 2 times sum to {N - 1} from {k = 0} X(k) sin({%pi (n+1)(2k + 1)} over 2N), n = 0,...,N - 1 .

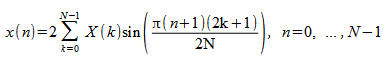Calling the forward and inverse routines will result in the original input scaled by 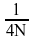image:1 over 4N .

`V[D]SINQF`: Forward FST of One or More Quarter-Wave Odd Sequences

The forward FST of one or more quarter-wave odd sequences is computed as

For i = 0, M - 1

image:X(i,k) = 1 over sqrt 4N times [ 2 sum to {N - 2} from {n = 0} x(n,i) sin ({%pi (n+1)(2k+1)} over 2N ) + x(N - 1,i) cos %pi k ], k = 0, ...,N - 1 .

V[D]SINQF Notes:

The input and output sequences are stored row-wise.
The transform is normalized so that if the inverse routine V[D]SINQB is called immediately after calling V[D]SINQF, the original data is obtained.

`V[D]SINQB`: Inverse FST of One or More Quarter-Wave Odd Sequences

The inverse FST of one or more quarter-wave odd sequences is computed as

For i = 0, M - 1

image:x(n,i) = 4 over sqrt 4N times sum to {N - 1} from {k = 0} X(k,i) sin ({%pi (n+1)(2k+1)} over 2N ), n = 0, ...,N - 1 .

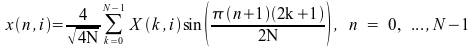V[D]SINQB Notes:

The input and output sequences are stored row-wise.
The transform is normalized, so that if V[D]SINQB is called immediately after calling V[D]SINQF, the original data is obtained.

Fast Cosine Transform Examples

Example 15 calls COST to compute the FCT and the inverse transform of a real even sequence. If the real sequence is of length 2N, only N + 1 input data points need to be stored and the number of resulting data points is also N + 1. The results are stored in the input array.

Example 15 Computer FCT and Inverse FCT of Single Real Even Sequence

my_system% cat cost.f
       program Drive cost
       implicit none
       integer,parameter :: len=4
       real x(0:len),work(3*(len+1)+15), z(0:len), scale
       integer i
       scale = 1.0/(2.0*len)
       call RANDOM_NUMBER(x(0:len))
       z(0:len) = x(0:len)
         write(*,'(a25,i1,a10,i1,a12)')'Input sequence of length ',
     $          len,' requires ', len+1,' data points'
       write(*,'(5(f8.3,2x),/)')(x(i),i=0,len)
       call costi(len+1, work)
       call cost(len+1, z, work)
       write(*,*)'Forward fast cosine transform'
       write(*,'(5(f8.3,2x),/)')(z(i),i=0,len)
       call cost(len+1, z, work)
       write(*,*)
     $    'Inverse fast cosine transform (results scaled by 1/2*N)'
       write(*,'(5(f8.3,2x),/)')(z(i)*scale,i=0,len)
       end
my_system% f95 -dalign cost.f -library=sunperf
my_system% a.out
Input sequence of length 4 requires 5 data points
0.557 0.603 0.210 0.352 0.867
Forward fast cosine transform
3.753 0.046 1.004 -0.666 -0.066
Inverse fast cosine transform (results scaled by 1/2*N)
0.557 0.603 0.210 0.352 0.867

Example 16 calls VCOSQF and VCOSQB to compute the FCT and the inverse FCT, respectively, of two real quarter-wave even sequences. If the real sequences are of length 2N, only N input data points need to be stored, and the number of resulting data points is also N. The results are stored in the input array.

Example 16 Compute the FCT and the Inverse FCT of Two Real Quarter-wave Even Sequences

my_system% cat vcosq.f
    program vcosq
    implicit none
    integer,parameter :: len=4, m = 2, ld = m+1
    real x(ld,len),xt(ld,len),work(3*len+15), z(ld,len)
    integer i, j
    call RANDOM_NUMBER(x)
    z = x
    write(*,'(a27,i1)')' Input sequences of length ',len
    do j = 1,m
       write(*,'(a3,i1,a4,4(f5.3,2x),a1,/)')
 $     'seq',j,' = (',(x(j,i),i=1,len),')'
    end do
    call vcosqi(len, work)
    call vcosqf(m,len, z, xt, ld, work)
    write(*,*)
 $ 'Forward fast cosine transform for quarter-wave even sequences'
    do j = 1,m
       write(*,'(a3,i1,a4,4(f5.3,2x),a1,/)')
 $     'seq',j,' = (',(z(j,i),i=1,len),')'
    end do
    call vcosqb(m,len, z, xt, ld, work)
    write(*,*)
 $  'Inverse fast cosine transform for quarter-wave even sequences'
  
    write(*,*)'(results are normalized)'
    do j = 1,m
       write(*,'(a3,i1,a4,4(f5.3,2x),a1,/)')
 $     'seq',j,' = (',(z(j,i),i=1,len),')'
    end do
    end
 
my_system% f95 -dalign vcosq.f -library=sunperf
my_system% a.out
Input sequences of length 4
seq1 = (0.557 0.352 0.990 0.539 )
seq2 = (0.603 0.867 0.417 0.156 )
Forward fast cosine transform for quarter-wave even sequences
seq1 = (0.755 -.392 -.029 0.224 )
seq2 = (0.729 0.097 -.091 -.132 )
Inverse fast cosine transform for quarter-wave even sequences
(results are normalized)
seq1 = (0.557 0.352 0.990 0.539 )
seq2 = (0.603 0.867 0.417 0.156 )

Fast Sine Transform Examples

In the following example Example 17, SINT is called to compute the FST and the inverse transform of a real odd sequence. If the real sequence is of length 2N, only N - 1 input data points need to be stored and the number of resulting data points is also N - 1. The results are stored in the input array.

Example 17 Compute the FCT and the Inverse FCT of Two Real Quarter-wave Even Sequences

my_system% cat sint.f
      program Drive sint
      implicit none
      integer,parameter :: len=4
      real x(0:len-2),work(3*(len-1)+15), z(0:len-2), scale
      integer i
      call RANDOM_NUMBER(x(0:len-2))
      z(0:len-2) = x(0:len-2)
      scale = 1.0/(2.0*len)  
      write(*,'(a25,i1,a10,i1,a12)')'Input sequence of length ',
    $       len,' requires ', len-1,' data points'   
      write(*,'(3(f8.3,2x),/)')(x(i),i=0,len-2)
      call sinti(len-1, work)
      call sint(len-1, z, work)
      write(*,*)'Forward fast sine transform'  
      write(*,'(3(f8.3,2x),/)')(z(i),i=0,len-2)
 
      call sint(len-1, z, work)
      write(*,*)
     $ 'Inverse fast sine transform (results scaled by 1/2*N)' 
      write(*,'(3(f8.3,2x),/)')(z(i)*scale,i=0,len-2)
      end
my_system% f95 -dalign sint.f -library=sunperf
my_system% a.out
Input sequence of length 4 requires 3 data points
0.557 0.603 0.210
Forward fast sine transform
2.291 0.694 -0.122
Inverse fast sine transform (results scaled by 1/2*N)
0.557 0.603 0.210

In the following example Example 18, VSINQF and VSINQB are called to compute the FST and inverse FST, respectively, of two real quarter-wave odd sequences. If the real sequence is of length 2N, only N input data points need to be stored and the number of resulting data points is also N. The results are stored in the input array.

Example 18 Compute FST and Inverse FST of Two Real Quarter-Wave Odd Sequences

my_system% cat vsinq.f
      program vsinq
      implicit none
      integer,parameter :: len=4, m = 2, ld = m+1
      real x(ld,len),xt(ld,len),work(3*len+15), z(ld,len)
      integer i, j
      call RANDOM_NUMBER(x)
      z = x
      write(*,'(a27,i1)')' Input sequences of length ',len
      do j = 1,m
         write(*,'(a3,i1,a4,4(f5.3,2x),a1,/)')
     $         'seq',j,' = (',(x(j,i),i=1,len),')'
      end do
      call vsinqi(len, work)
      call vsinqf(m,len, z, xt, ld, work)
      write(*,*)
    $ 'Forward fast sine transform for quarter-wave odd sequences'
      do j = 1,m
      write(*,'(a3,i1,a4,4(f5.3,2x),a1,/)')
    $       'seq',j,' = (',(z(j,i),i=1,len),')'
      end do
 
      call vsinqb(m,len, z, xt, ld, work)
      write(*,*)
    $ 'Inverse fast sine transform for quarter-wave odd sequences'
      write(*,*)'(results are normalized)'
      do j = 1,m
      write(*,'(a3,i1,a4,4(f5.3,2x),a1,/)')
    $       'seq',j,' = (',(z(j,i),i=1,len),')'
      end do 
      end
my_system% f95 vsinq.f -library=sunperf
my_system% a.out
Input sequences of length 4
seq1 = (0.557 0.352 0.990 0.539 )
seq2 = (0.603 0.867 0.417 0.156 )
Forward fast sine transform for quarter-wave odd sequences
seq1 = (0.823 0.057 0.078 0.305 )
seq2 = (0.654 0.466 -.069 -.037 )
Inverse fast sine transform for quarter-wave odd sequences
(results are normalized)
seq1 = (0.557 0.352 0.990 0.539 )
seq2 = (0.603 0.867 0.417 0.156 )