Forward and Inverse FFT Routines

The following tables list the names of the FFT routines and their calling sequence. Double precision routine names are in square brackets. See the individual man pages for detailed information on the data type and size of the arguments.

• Table 9

• Table 10

• Table 11

Table 9  FFT Linear Routines and Their Arguments

Routine Name Arguments CFFTS [ZFFTD] (OPT, N1, SCALE, X, Y, TRIGS, IFAC, WORK, LWORK, ERR) SFFTC [DFFTZ] (OPT, N1, SCALE, X, Y, TRIGS, IFAC, WORK, LWORK, ERR) CFFTSM [ZFFTDM] (OPT, N1, N2, SCALE, X, LDX1, Y, LDY1, TRIGS, IFAC, WORK, LWORK, ERR) SFFTCM [DFFTZM] (OPT, N1, N2, SCALE, X, LDX1, Y, LDY1, TRIGS, IFAC, WORK, LWORK, ERR) CFFTC [ZFFTZ] (OPT, N1, SCALE, X, Y, TRIGS, IFAC, WORK, LWORK, ERR) CFFTCM [ZFFTZM] (OPT, N1, N2, SCALE, X, LDX1, Y, LDY1, TRIGS, IFAC, WORK, LWORK, ERR)

Table 10  FFT Two-Dimensional Routines and Their Arguments

Routine Name Arguments CFFTS2 [ZFFTD2] (OPT, N1, N2, SCALE, X, LDX1, Y, LDY1, TRIGS, IFAC, WORK, LWORK, ERR) SFFTC2 [DFFTZ2] (OPT, N1, N2, SCALE, X, LDX1, Y, LDY1, TRIGS, IFAC, WORK, LWORK, ERR) CFFTC2 [ZFFTZ2] (OPT, N1, N2, SCALE, X, LDX1, Y, LDY1, TRIGS, IFAC, WORK, LWORK, ERR)

Table 11  FFT Three-Dimensional Routines and Their Arguments

Routine Name Arguments CFFTS3 [ZFFTD3] (OPT, N1, N2, N3, SCALE, X, LDX1, LDX2, Y, LDY1, LDY2, TRIGS, IFAC, WORK, LWORK, ERR) SFFTC3 [DFFTZ3] (OPT, N1, N2, N3, SCALE, X, LDX1, LDX2, Y, LDY1, LDY2, TRIGS, IFAC, WORK, LWORK, ERR) CFFTC3 [ZFFTZ3] (OPT, N1, N2, N3, SCALE, X, LDX1, LDX2, Y, LDY1, LDY2, TRIGS, IFAC, WORK, LWORK, ERR)

Oracle Developer Studio Performance Library FFT routines use the following arguments.

• OPT: Flag indicating whether the routine is called to initialize or to compute the transform.

• N1, N2, N3: Problem dimensions for one, two, and three dimensional transforms.

• X: Input array where X is of type COMPLEX if the routine is a complex-to-complex transform or a complex-to-real transform. X is of type REAL for a real-to-complex transform.

• Y: Output array where Y is of type COMPLEX if the routine is a complex-to-complex transform or a real-to-complex transform. Y is of type REAL for a complex-to-real transform.

• LDX1, LDX2 and LDY1, LDY2: LDX1 and LDX2 are the leading dimensions of the input array, and LDY1 and LDY2 are the leading dimensions of the output array. The FFT routines allow the output to overwrite the input, which is an in-place transform, or to be stored in a separate array apart from the input array, which is an out‐of‐place transform. In complex-to-complex transforms, the input data is of the same size as the output data. However, real-to-complex and complex-to-real transforms have different memory requirements for input and output data. Care must be taken to ensure that the input array is large enough to accommodate the transform results when computing an in-place transform.

• TRIGS: Array containing the trigonometric weights.

• IFAC: Array containing factors of the problem dimensions. The problem sizes are as follows:

  • Linear FFT: Problem size of dimension N1

  • Two-dimensional FFT: Problem size of dimensions N1 and N2

  • Three-dimensional FFT: Problem size of dimensions N1, N2, and N3

  While N1, N2, and N3 can be of any size, a real-to-complex or a complex-to-real transform can be computed most efficiently when

  ,

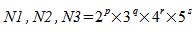  and a complex-to-complex transform can be computed most efficiently when

  ,

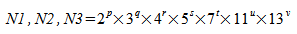  where p, q, r, s, t, u, and v are integers and p, q, r, s, t, u, v ≥ 0.

• WORK: Workspace whose size depends on the routine and the number of threads that are being used to compute the transform if the routine is parallelized.

• LWORK: Size of workspace. If LWORK is zero, the routine will allocate a workspace with the required size.

• SCALE: A scalar with which the output is scaled. Occasionally in literature, the inverse transform is defined with a scaling factor of 1/N1 for one-dimensional transforms, 1/(N1 × N2) for two-dimensional transforms, and 1/(N1 × N2 × N3) for three-dimensional transforms. In such case, the inverse transform is said to be normalized. If a normalized FFT is followed by its inverse FFT, the result is the original input data. The Oracle Developer Studio Performance Library FFT routines are not normalized. However, normalization can be done easily by calling the inverse FFT routine with the appropriate scaling factor stored in SCALE.

• ERR: A flag returning a nonzero value if an error is encountered in the routine and zero otherwise.

Linear FFT Routines

Linear FFT routines compute the FFT of real or complex data in one dimension only. The data can be one or more complex or real sequences. For a single sequence, the data is stored in a vector. If more than one sequence is being transformed, the sequences are stored column-wise in a two-dimensional array and a one-dimensional FFT is computed for each sequence along the column direction. The linear forward FFT routines compute: 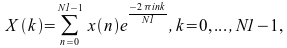where .

Or expressed in polar form: .

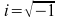The inverse FFT routines compute

In polar form:

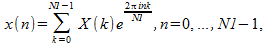
With the forward transform, if the input is one or more complex sequences of size N1, the result will be one or more complex sequences, each consisting of N1 unrelated data points. However, if the input is one or more real sequences, each containing N1 real data points, the result will be one or more complex sequences that are conjugate symmetric. That is:

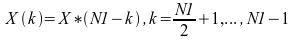
The imaginary part of X(0) is always zero. If N1 is even, the imaginary part of 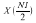is also zero. Both zeros are stored explicitly. Because the second half of each sequence can be derived from the first half, only 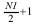complex data points are computed and stored in the output array. Here and elsewhere in this chapter, integer division is rounded down.

With the inverse transform, if an N1-point complex-to-complex transform is being computed, then N1 unrelated data points are expected in each input sequence and N1 data points will be returned in the output array. However, if an N1-point complex-to-real transform is being computed, only the first 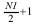complex data points of each conjugate symmetric input sequence are expected in the input, and the routine will return N1 real data points in each output sequence.

For each value of N1, either the forward or the inverse routine must be called to compute the factors of N1 and the trigonometric weights associated with those factors before computing the actual FFT. The factors and trigonometric weights can be reused in subsequent transforms as long as N1 remains unchanged.

The following table Table 12 lists the single precision linear FFT routines and their purposes. For routines that have two-dimensional arrays as input and output, Table 12 also lists the leading dimension requirements. The same information applies to the corresponding double precision routines except that their data types are double precision and double complex. See Table 12 for the mapping. See the individual man pages for a complete description of the routines and their arguments.

Table 12  Single Precision Linear FFT Routines

Name Purpose Size and Type of Input Size and Type of Output Leading Dimension Requirements SFFTC OPT = 0 initialization OPT = -1 real-to-complex forward linear FFT of a single vector N1, Real , Complex SFFTC OPT = 0 initialization OPT = 1 complex-to-real inverse linear FFT of single vector , Complex N1 Real CFFTC OPT = 0 initialization OPT = -1 complex-to-complex forward linear FFT of a single vector N1, Complex N1, Complex OPT = 1 complex-to-complex inverse linear FFT of a single vector N1, Complex N1, Complex SFFTCM OPT = 0 initialization OPT = -1 real-to-complex forward linear FFT of M vectors N1 × M, Real , Complex LDX1 = 2 × LDY1 LDX1 ≥ N1 CFFTSM OPT = 0 initialization OPT = 1 complex-to-real inverse linear FFT of M vectors , Complex N1 × M, Real LDX1 ≥ LDY1=2 × LDX1 LDX1 ≥ LDY1 ≥ N1 CFFTCM OPT = 0 initialization OPT = -1 complex-to-complex forward linear FFT of M vectors N1 × M, Complex N1 × M, Complex LDX1 ≥ N1 LDY1 ≥ N1 LDX1 ≥ N1 LDY1 ≥ N1 OPT = 1 complex-to-complex inverse linear FFT of M vectors N1 × M, Complex N1 × M, Complex LDX1 ≥ N1 LDY1 ≥ N1 LDX1 ≥ N1 LDY1 ≥ N1

The following example shows how to compute the linear real-to-complex and complex-to-real FFT of a set of sequences.

Example 10  Linear Real-to-Complex FFT and Complex-to-Real FFT

my_system% cat testscm.f
       PROGRAM TESTSCM
       IMPLICIT NONE
       INTEGER :: LW, IERR, I, J, K, LDX, LDC
       INTEGER,PARAMETER :: N1 = 3, N2 = 2, LDZ = N1, 
      $        LDC = N1, LDX = 2*LDC
       INTEGER, DIMENSION(:) :: IFAC(128)
       REAL :: SCALE
       REAL, PARAMETER :: ONE = 1.0
       REAL, DIMENSION(:) :: SW(N1), TRIGS(2*N1)
       REAL, DIMENSION(0:LDX-1,0:N2-1) :: X, V, Y
       COMPLEX, DIMENSION(0:LDZ-1, 0:N2-1) :: Z
* workspace size	
       LW = N1
       SCALE = ONE/N1
       WRITE(*,*)	
      $ 'Linear complex-to-real and real-to-complex FFT of a sequence'
       WRITE(*,*)
       X = RESHAPE(SOURCE = (/.1, .2, .3,0.0,0.0,0.0,7.,8.,9.,
      $    0.0, 0.0, 0.0/), SHAPE=(/6,2/))	 
       V = X
       WRITE(*,*) 'X = '
       DO I = 0,N1-1
         WRITE(*,'(2(F4.1,2x))') (X(I,J), J = 0, N2-1)
       END DO
       WRITE(*,*)
* intialize trig table and compute factors of N1
       CALL SFFTCM(0, N1, N2, ONE, X, LDX, Z, LDZ, TRIGS, IFAC, 
      $ SW, LW, IERR)
       IF (IERR .NE. 0) THEN 
          PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
          STOP
       END IF
 
* Compute out-of-place forward linear FFT.
* Let FFT routine allocate memory.
       CALL SFFTCM(-1, N1, N2, ONE, X, LDX, Z, LDZ, TRIGS, IFAC,
      $            SW, 0, IERR)
      IF (IERR .NE. 0) THEN
        PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
        STOP 
      END IF
      WRITE(*,*) 'out-of-place forward FFT of X:'
      WRITE(*,*)'Z ='
      DO I = 0, N1/2
         WRITE(*,'(2(A1, F4.1,A1,F4.1,A1,2x))') ('(',REAL(Z(I,J)),
     $ ',',AIMAG(Z(I,J)),')', J = 0, N2-1)
      END DO
      WRITE(*,*)
* Compute in-place forward linear FFT.
* X must be large enough to store N1/2+1 complex values
      CALL SFFTCM(-1, N1, N2, ONE, X, LDX, X, LDC, TRIGS, IFAC,
     $            SW, LW, IERR)
      IF (IERR .NE. 0) THEN
         PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
         STOP
      END IF
      WRITE(*,*) 'in-place forward FFT of X:'
      CALL PRINT_REAL_AS_COMPLEX(N1/2+1, N2, 1, X, LDC, N2)
      WRITE(*,*)
* Compute out-of-place inverse linear FFT.
      CALL CFFTSM(1, N1, N2, SCALE, Z, LDZ, X, LDX, TRIGS, IFAC,
     $            SW, LW, IERR)
      IF (IERR .NE. 0) THEN
         PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
         STOP
      END IF
      WRITE(*,*) 'out-of-place inverse FFT of Z:'
      DO I = 0, N1-1
         WRITE(*,'(2(F4.1,2X))') (X(I,J), J = 0, N2-1)
      END DO
      WRITE(*,*)
* Compute in-place inverse linear FFT.
      CALL CFFTSM(1, N1, N2, SCALE, Z, LDZ, Z, LDZ*2, TRIGS,
     $            IFAC, SW, 0, IERR)
      IF (IERR .NE. 0) THEN
         PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
         STOP 
      END IF
 
      WRITE(*,*) 'in-place inverse FFT of Z:'
      CALL PRINT_COMPLEX_AS_REAL(N1, N2, 1, Z, LDZ*2, N2)
      WRITE(*,*)
      END PROGRAM TESTSCM
      SUBROUTINE PRINT_COMPLEX_AS_REAL(N1, N2, N3, A, LD1, LD2) 
      INTEGER N1, N2, N3, I, J, K
      REAL A(LD1, LD2, *)
      DO K = 1, N3
         DO I = 1, N1
            WRITE(*,'(5(F4.1,2X))') (A(I,J,K), J = 1, N2)
         END DO 
         WRITE(*,*)
      END DO
      END
      SUBROUTINE PRINT_REAL_AS_COMPLEX(N1, N2, N3, A, LD1, LD2)
      INTEGER N1, N2, N3, I, J, K
      COMPLEX A(LD1, LD2, *)
      DO K = 1, N3
         DO I = 1, N1
            WRITE(*,'(5(A1, F4.1,A1,F4.1,A1,2X))') ('(',REAL(A(I,J,K)),
     $            ',',AIMAG(A(I,J,K)),')', J = 1, N2)
         END DO
         WRITE(*,*)
      END DO
      END
my_system% f95 -dalign testscm.f -xlibrary=sunperf
my_system% a.out
Linear complex-to-real and real-to-complex FFT of a sequence
X =
0.1 7.0
0.2 8.0
0.3 9.0
out-of-place forward FFT of X:
Z =
( 0.6, 0.0) (24.0, 0.0)
(-0.2, 0.1) (-1.5, 0.9)
in-place forward FFT of X:
( 0.6, 0.0) (24.0, 0.0)
(-0.2, 0.1) (-1.5, 0.9)
out-of-place inverse FFT of Z:
0.1 7.0
0.2 8.0
0.3 9.0
 
in-place inverse FFT of Z:
0.1 7.0
0.2 8.0
0.3 9.0

Example 7-1 Notes:

The forward FFT of X is actually:

Because of symmetry, Z(2) is the complex conjugate of Z(1), and therefore only the first two 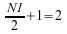complex values are stored. For the in-place forward transform, SFFTCM is called with real array X as the input and output. Because SFFTCM expects the output array to be of type COMPLEX, the leading dimension of X as an output array must be as if X were complex. Since the leading dimension of real array X is LDX = 2 × LDC, the leading dimension of X as a complex output array must be LDC. Similarly, in the in-place inverse transform, CFFTSM is called with complex array Z as the input and output. Because CFFTSM expects the output array to be of type REAL, the leading dimension of Z as an output array must be as if Z were real. Since the leading dimension of complex array Z is LDZ, the leading dimension of Z as a real output array must be LDZ × 2.

The following example Example 11 shows how to compute the linear complex-to-complex FFT of a set of sequences.

Example 11  Linear Complex-to-Complex FFT

my_system% cat testccm.f
       PROGRAM TESTCCM
       IMPLICIT NONE
       INTEGER :: LDX1, LDY1, LW, IERR, I, J, K, LDZ1, NCPUS,
      $           USING_THREADS, IFAC(128)
       INTEGER, PARAMETER :: N1 = 3, N2 = 4, LDX1 = N1, LDZ1 = N1,
      $                      LDY1 = N1+2
       REAL, PARAMETER :: ONE = 1.0, SCALE = ONE/N1
       COMPLEX :: Z(0:LDZ1-1,0:N2-1), X(0:LDX1-1,0:N2-1),
      $           Y(0:LDY1-1,0:N2-1)
 
       REAL :: TRIGS(2*N1)
       REAL, DIMENSION(:), ALLOCATABLE :: SW
* get number of threads 
       NCPUS = USING_THREADS()
* workspace size
       LW = 2 * N1 * NCPUS
       WRITE(*,*)'Linear complex-to-complex FFT of one or more sequences'
       WRITE(*,*)
       ALLOCATE(SW(LW))
       X = RESHAPE(SOURCE =(/(.1,.2),(.3,.4),(.5,.6),(.7,.8),(.9,1.0),
      $ (1.1,1.2),(1.3,1.4),(1.5,1.6),(1.7,1.8),(1.9,2.0),(2.1,2.2),
      $ (1.2,2.0)/), SHAPE=(/LDX1,N2/))
       Z = X
       WRITE(*,*) 'X = '
       DO I = 0, N1-1
          WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))') ('(',REAL(X(I,J)),
      $           ',',AIMAG(X(I,J)),')', J = 0, N2-1)
       END DO	
       WRITE(*,*)* intialize trig table and compute factors of N1
       CALL CFFTCM(0, N1, N2, SCALE, X, LDX1, Y, LDY1, TRIGS, IFAC,
      $            SW, LW, IERR)
       IF (IERR .NE. 0) THEN
         PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
         STOP
       END IF
* Compute out-of-place forward linear FFT.
* Let FFT routine allocate memory.
       CALL CFFTCM(-1, N1, N2, ONE, X, LDX1, Y, LDY1, TRIGS, IFAC,
      $            SW, 0, IERR)
       IF (IERR .NE. 0) THEN
          PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
          STOP
       END IF
* Compute in-place forward linear FFT. LDZ1 must equal LDX1
       CALL CFFTCM(-1, N1, N2, ONE, Z, LDX1, Z, LDZ1, TRIGS,
      $            IFAC, SW, 0, IERR)
       WRITE(*,*) 'in-place forward FFT of X:'
       DO I = 0, N1-1 
          WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))') ('(',REAL(Z(I,J)),
      $           ',',AIMAG(Z(I,J)),')', J = 0, N2-1)
       END DO
 
       WRITE(*,*)
       WRITE(*,*) 'out-of-place forward FFT of X:'
       WRITE(*,*) 'Y ='
       DO I = 0, N1-1
          WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))') ('(',REAL(Y(I,J)),
      $        ',',AIMAG(Y(I,J)),')', J = 0, N2-1)
       END DO
       WRITE(*,*)
* Compute in-place inverse linear FFT.
       CALL CFFTCM(1, N1, N2, SCALE, Y, LDY1, Y, LDY1, TRIGS, IFAC,
      $            SW, LW, IERR)
       IF (IERR .NE. 0) THEN
          PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
          STOP
       END IF
       WRITE(*,*) 'in-place inverse FFT of Y:'
       WRITE(*,*) 'Y ='
       DO I = 0, N1-1
          WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))') ('(',REAL(Y(I,J)),
      $           ',',AIMAG(Y(I,J)),')', J = 0, N2-1)
       END DO
       DEALLOCATE(SW)
       END PROGRAM TESTCCM
my_system% f95 -dalign testccm.f -library=sunperf
my_system% a.out
Linear complex-to-complex FFT of one or more sequences
X =
( 0.1, 0.2) ( 0.7, 0.8) ( 1.3, 1.4) ( 1.9, 2.0)
( 0.3, 0.4) ( 0.9, 1.0) ( 1.5, 1.6) ( 2.1, 2.2)
( 0.5, 0.6) ( 1.1, 1.2) ( 1.7, 1.8) ( 1.2, 2.0)
in-place forward FFT of X:
(  0.9,  1.2) (  2.7,  3.0) (  4.5,  4.8) ( 5.2,  6.2)
( -0.5, -0.1) ( -0.5, -0.1) ( -0.5, -0.1) ( 0.4, -0.9)
( -0.1, -0.5) ( -0.1, -0.5) ( -0.1, -0.5) ( 0.1,  0.7)
out-of-place forward FFT of X:
Y = 
(  0.9,  1.2) (  2.7,  3.0) (  4.5,  4.8) ( 5.2,  6.2)
( -0.5, -0.1) ( -0.5, -0.1) ( -0.5, -0.1) ( 0.4, -0.9)
( -0.1, -0.5) ( -0.1, -0.5) ( -0.1, -0.5) ( 0.1,  0.7)
in-place inverse FFT of Y:
Y = 
( 0.1, 0.2) ( 0.7, 0.8) ( 1.3, 1.4) ( 1.9, 2.0)
( 0.3, 0.4) ( 0.9, 1.0) ( 1.5, 1.6) ( 2.1, 2.2)
( 0.5, 0.6) ( 1.1, 1.2) ( 1.7, 1.8) ( 1.2, 2.0)
 
 

Two-Dimensional FFT Routines

For the linear FFT routines, when the input is a two-dimensional array, the FFT is computed along one dimension only, namely, along the columns of the array. The two-dimensional FFT routines take a two-dimensional array as input and compute the FFT along both the column and row dimensions. Specifically, the forward two-dimensional FFT routines compute the following:

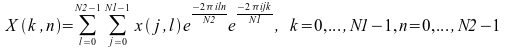
The inverse two-dimensional FFT routines compute the following:

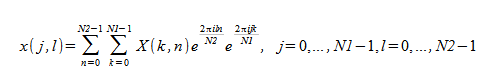
For both the forward and inverse two-dimensional transforms, a complex-to-complex transform where the input problem is N1 × N2 will yield a complex array that is also N1 × N2.

When computing a real-to-complex two-dimensional transform (forward FFT), if the real input array is of dimensions N1 × N2, the result will be a complex array of dimensions .

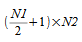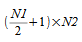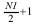Conversely, when computing a complex-to-real transform (inverse FFT) of dimensions N1 × N2, an complex array is required as input. As with the real-to-complex and complex-to-real linear FFT, because of conjugate symmetry, only the first complex data points need to be stored in the input or output array along the first dimension. The complex subarray 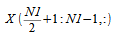can be obtained from 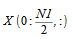as follows:

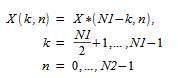
To compute a two-dimensional transform, an FFT routine must be called twice. One call initializes the routine and the second call actually computes the transform. The initialization includes computing the factors of N1 and N2 and the trigonometric weights associated with those factors. In subsequent forward or inverse transforms, initialization is not necessary as long as N1 and N2 remain unchanged.

IMPORTANT: Upon returning from a two-dimensional FFT routine, Y(0 : N - 1, :) contains the transform results and the original contents of Y(N : LDY-1, :) is overwritten. Here, N = N1 in the complex-to-complex and complex-to-real transforms and N = 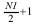in the real-to-complex transform.

The following table Table 13 lists the single precision two-dimensional FFT routines and their purposes. The same information applies to the corresponding double precision routines except that their data types are double precision and double complex. See Table 13 for the mapping. Refer to the individual man pages for a complete description of the routines and their arguments.

Table 13  Single Precision Two-Dimensional FFT Routines

Name Purpose Size, Type of Input Size, Type of Output Leading Dimension Requirements SFFTC2 OPT = 0 initialization OPT = -1 real-to-complex forward two-dimensional FFT N1 × N2, Real , Complex LDX1 = 2 × LDY1 LDY1 ≥ LDX1 ≥ N1 LDY1 ≥ CFFTS2 OPT = 0 initialization OPT = 1 complex-to-real inverse two-dimensional FFT , Complex N1 × N2, Real LDX1 ≥ LDY1=2 × LDX1 LDX1 ≥ LDY1≥ 2 × LDX1 LDY1 is even CFFTC2 OPT = 0 initialization OPT = -1 complex-to-complex forward two-dimensional FFT N1 × N2, Complex N1 × N2, Complex LDX1 ≥ N1 LDY1 = LDX1 LDX1 ≥ N1 LDY1 ≥ N1 OPT = 1 complex-to-complex inverse two-dimensional FFT N1 × N2, Complex N1 × N2, Complex LDX1 ≥ N1 LDY1 = LDX1 LDX1 ≥ N1 LDY1 = LDX1

Example 12  Two-Dimensional Real-to-Complex FFT and Complex-to-Real FFT of a Two-Dimensional Array

The following example shows how to compute a two-dimensional real-to-complex FFT and complex-to-real FFT of a two-dimensional array.

my_system% cat testsc2.f
       PROGRAM TESTSC2
       IMPLICIT NONE
       INTEGER, PARAMETER :: N1 = 3, N2 = 4, LDX1 = N1,
      $         LDY1 = N1/2+1, LDR1 = 2*(N1/2+1)
       INTEGER LW, IERR, I, J, K, IFAC(128*2)
       REAL, PARAMETER :: ONE = 1.0, SCALE = ONE/(N1*N2)
       REAL :: V(LDR1,N2), X(LDX1, N2), Z(LDR1,N2),
      $        SW(2*N2), TRIGS(2*(N1+N2))
       COMPLEX :: Y(LDY1,N2)
       WRITE(*,*) $'Two-dimensional complex-to-real and real-to-complex FFT'
       WRITE(*,*)
       X = RESHAPE(SOURCE = (/.1, .2, .3, .4, .5, .6, .7, .8,
      $            2.0,1.0, 1.1, 1.2/), SHAPE=(/LDX1,N2/))
       DO I = 1, N2
          V(1:N1,I) = X(1:N1,I)
       END DO
       WRITE(*,*) 'X ='
       DO I = 1, N1
          WRITE(*,'(5(F5.1,2X))') (X(I,J), J = 1, N2)
       END DO
       WRITE(*,*)
* Initialize trig table and get factors of N1, N2
       CALL SFFTC2(0,N1,N2,ONE,X,LDX1,Y,LDY1,TRIGS,
      $            IFAC,SW,0,IERR)
* Compute 2-dimensional out-of-place forward FFT.
* Let FFT routine allocate memory.
* cannot do an in-place transform in X because LDX1 < 2*(N1/2+1)
       CALL SFFTC2(-1,N1,N2,ONE,X,LDX1,Y,LDY1,TRIGS,
      $            IFAC,SW,0,IERR)
       WRITE(*,*) 'out-of-place forward FFT of X:'
       WRITE(*,*)'Y ='
       DO I = 1, N1/2+1
          WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))')('(',REAL(Y(I,J)),
      $           ',',AIMAG(Y(I,J)),')', J = 1, N2)
       END DO
       WRITE(*,*)
 
* Compute 2-dimensional in-place forward FFT. 
* Use workspace already allocated. 
* V which is real array containing input data is also 
* used to store complex results; as a complex array, its first 
* leading dimension is LDR1/2.
       CALL SFFTC2(-1,N1,N2,ONE,V,LDR1,V,LDR1/2,TRIGS,
      $            IFAC,SW,LW,IERR)
       WRITE(*,*) 'in-place forward FFT of X:'
       CALL PRINT_REAL_AS_COMPLEX(N1/2+1, N2, 1, V, LDR1/2, N2)
* Compute 2-dimensional out-of-place inverse FFT. 
* Leading dimension of Z must be even
       CALL CFFTS2(1,N1,N2,SCALE,Y,LDY1,Z,LDR1,TRIGS, 
      $            IFAC,SW,0,IERR)
       WRITE(*,*) 'out-of-place inverse FFT of Y:'
       DO I = 1, N1
          WRITE(*,'(5(F5.1,2X))') (Z(I,J), J = 1, N2)
       END DO
       WRITE(*,*)
* Compute 2-dimensional in-place inverse FFT.
* Y which is complex array containing input data is also 
* used to store real results; as a real array, its first
* leading dimension is 2*LDY1.
       CALL CFFTS2(1,N1,N2,SCALE,Y,LDY1,Y,2*LDY1,
      $            TRIGS,IFAC,SW,0,IERR)
       WRITE(*,*) 'in-place inverse FFT of Y:'
       CALL PRINT_COMPLEX_AS_REAL(N1, N2, 1, Y, 2*LDY1, N2)
       END PROGRAM TESTSC2
       SUBROUTINE PRINT_COMPLEX_AS_REAL(N1, N2, N3, A, LD1, LD2)
       INTEGER N1, N2, N3, I, J, K
       REAL A(LD1, LD2, *)
       DO K = 1, N3
          DO I = 1, N1
             WRITE(*,'(5(F5.1,2X))') (A(I,J,K), J = 1, N2)
          END DO 
          WRITE(*,*)
       END DO
       END
 
       SUBROUTINE PRINT_REAL_AS_COMPLEX(N1, N2, N3, A, LD1, LD2)
       INTEGER N1, N2, N3, I, J, K 
       COMPLEX A(LD1, LD2, *)
       DO K = 1, N3 
          DO I = 1, N1 
             WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))') ('(',REAL(A(I,J,K)),
      $              ',',AIMAG(A(I,J,K)),')', J = 1, N2)
          END DO
          WRITE(*,*)
       END DO
       END
my_system% f95 -dalign testsc2.f -library=sunperf
my_system% a.out
Two-dimensional complex-to-real and real-to-complex FFT
x =
0.1 0.4 0.7 1.0
0.2 0.5 0.8 1.1
0.3 0.6 2.0 1.2
out-of-place forward FFT of X:
Y =
(  8.9, 0.0) ( -2.9,  1.8) ( -0.7, 0.0) ( -2.9, -1.8)
( -1.2, 1.3) (  0.5, -1.0) ( -0.5, 1.0) (  0.5, -1.0)
in-place forward FFT of X:
( 8.9, 0.0) ( -2.9, 1.8) ( -0.7, 0.0) ( -2.9, -1.8)
( -1.2, 1.3) ( 0.5, -1.0) ( -0.5, 1.0) ( 0.5, -1.0)
out-of-place inverse FFT of Y:
0.1 0.4 0.7 1.0
0.2 0.5 0.8 1.1
0.3 0.6 2.0 1.2
in-place inverse FFT of Y:
0.1 0.4 0.7 1.0
0.2 0.5 0.8 1.1
0.3 0.6 2.0 1.2
 

Three-Dimensional FFT Routines

Oracle Developer Studio Performance Library includes routines that compute three-dimensional FFT. In this case, the FFT is computed along all three dimensions of a three-dimensional array. The forward FFT computes

,

and the inverse FFT computes

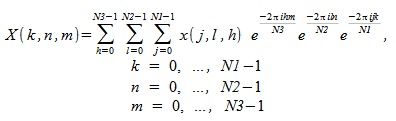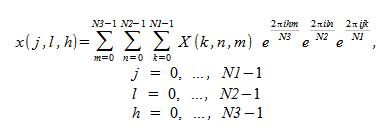
In the complex-to-complex transform, if the input problem is N1 × N2 × N3, a three-dimensional transform will yield a complex array that is also N1 × N2 × N3. When computing a real-to-complex three-dimensional transform, if the real input array is of dimensions N1 × N2 × N3, the result will be a complex array of dimensions 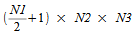. Conversely, when computing a complex-to-real FFT of dimensions N1 × N2 × N3, an 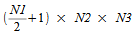complex array is required as input. 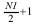As with the real-to-complex and complex-to-real linear FFT, because of conjugate symmetry, only the first complex data points need to be stored along the first dimension. The complex subarray 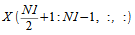can be obtained from 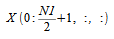as follows:

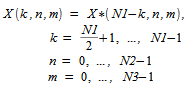
To compute a three-dimensional transform, an FFT routine must be called twice: Once to initialize and once more to actually compute the transform. The initialization includes computing the factors of N1, N2, and N3 and the trigonometric weights associated with those factors. In subsequent forward or inverse transforms, initialization is not necessary as long as N1, N2, and N3 remain unchanged.

IMPORTANT: Upon returning from a three-dimensional FFT routine, Y(0 : N - 1, :, :) contains the transform results and the original contents of Y(N:LDY1-1, :, :) is overwritten. Here, N=N1 in the complex-to-complex and complex-to-real transforms and N= 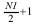in the real-to-complex transform.

Table 14 lists the single precision three-dimensional FFT routines and their purposes. The same information applies to the corresponding double precision routines except that their data types are double precision and double complex. See Table 14 for the mapping. See the individual man pages for a complete description of the routines and their arguments.

Table 14  Single Precision Three-Dimensional FFT Routines

Name Purpose Size, Type of Input Size, Type of Output Leading Dimension Requirements SFFTC3 OPT = 0 initialization OPT = -1 real-to-complex forward three-dimensional FFT N1 × N2 × N3, Real ,Complex LDX1=2 × LDY1 LDX2 ≥ N2 LDY1 ≥ LDY2 = LDX2 LDX1 ≥ N1 LDX2 ≥ N2 LDY1 ≥ LDY2 ≥ N2 CFFTS3 OPT = 0 initialization OPT = 1 complex-to-real inverse three-dimensional FFT , Complex N1 × N2 × N3, Real LDX1 ≥ LDX2 ≥ N2 LDY1=2 × LDX1 LDY2=LDX2 LDX1 ≥ LDX2 ≥ N2 LDY1 ≥ 2 × LDX1 LDY1 is even LDY2 ≥ N2 CFFTC3 OPT = 0 initialization OPT = -1 complex-to-complex forward three-dimensional FFT N1 × N2 × N3, Complex N1 × N2 × N3, Complex LDX1 ≥ N1 LDX2 ≥ N2 LDY1=LDX1 LDY2=LDX2 LDX1 ≥ N1 LDX2 ≥ N2 LDY1 ≥ N1 LDY2 ≥ N2 OPT = 1 complex-to-complex inverse three-dimensional FFT N1 × N2 × N3, Complex N1 × N2 × N3, Complex LDX1 ≥ N1 LDX2 ≥ N2 LDY1=LDX1 LDY2=LDX2 LDX1 ≥ N1 LDX2 ≥ N2 LDY1 ≥ N1 LDY2 ≥ N2

Example 7-4 shows how to compute the three-dimensional real-to-complex FFT and complex-to-real FFT of a three-dimensional array.

Example 13  Three-Dimensional Real-to-Complex FFT and Complex-to-Real FFT of a Three-Dimensional Array

my_system% cat testsc3.f
       PROGRAM TESTSC3
       IMPLICIT NONE
       INTEGER LW, NCPUS, IERR, I, J, K, USING_THREADS, IFAC(128*3)
       INTEGER, PARAMETER :: N1 = 3, N2 = 4, N3 = 2, LDX1 = N1, 
      $                      LDX2 = N2, LDY1 = N1/2+1, LDY2 = N2,
      $                      LDR1 = 2*(N1/2+1), LDR2 = N2
       REAL, PARAMETER :: ONE = 1.0, SCALE = ONE/(N1*N2*N3)
 
       REAL :: V(LDR1,LDR2,N3), X(LDX1,LDX2,N3), Z(LDR1,LDR2,N3),
      $        TRIGS(2*(N1+N2+N3))
       REAL, DIMENSION(:), ALLOCATABLE :: SW
       COMPLEX :: Y(LDY1,LDY2,N3)
       WRITE(*,*)
      $'Three-dimensional complex-to-real and real-to-complex FFT'
       WRITE(*,*)
* get number of threads
       NCPUS = USING_THREADS()
* compute workspace size required
       LW = (MAX(MAX(N1,2*N2),2*N3) + 16*N3) * NCPUS
       ALLOCATE(SW(LW))
       X = RESHAPE(SOURCE = 
      $    (/ .1, .2, .3, .4, .5, .6, .7, .8, .9,1.0,1.1,1.2,
      $     4.1,1.2,2.3,3.4,6.5,1.6,2.7,4.8,7.9,1.0,3.1,2.2/),
      $     SHAPE=(/LDX1,LDX2,N3/))
       V = RESHAPE(SOURCE =
      $    (/.1,.2,.3,0.,.4,.5,.6,0.,.7,.8,.9,0.,1.0,1.1,1.2,0.,
      $     4.1,1.2,2.3,0.,3.4,6.5,1.6,0.,2.7,4.8,7.9,0.,
      $     1.0,3.1,2.2,0./), SHAPE=(/LDR1,LDR2,N3/))
       WRITE(*,*) 'X ='
       DO K = 1, N3
          DO I = 1, N1
             WRITE(*,'(5(F5.1,2X))') (X(I,J,K), J = 1, N2)
          END DO
          WRITE(*,*)
       END DO
* Initialize trig table and get factors of N1, N2 and N3
       CALL SFFTC3(0,N1,N2,N3,ONE,X,LDX1,LDX2,Y,LDY1,LDY2,TRIGS,
      $            IFAC,SW,0,IERR)
* Compute 3-dimensional out-of-place forward FFT. 
* Let FFT routine allocate memory.
* cannot do an in-place transform because LDX1 < 2*(N1/2+1)
       CALL SFFTC3(-1,N1,N2,N3,ONE,X,LDX1,LDX2,Y,LDY1,LDY2,TRIGS,
      $            IFAC,SW,0,IERR)
       WRITE(*,*) 'out-of-place forward FFT of X:'
       WRITE(*,*)'Y ='
       DO K = 1, N3
          DO I = 1, N1/2+1
             WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))')('(',REAL(Y(I,J,K)),
      $              ',',AIMAG(Y(I,J,K)),')', J = 1, N2)
          END DO
          WRITE(*,*)
       END DO
 
* Compute 3-dimensional in-place forward FFT. 
* Use workspace already allocated.
* V which is real array containing input data is also
* used to store complex results; as a complex array, its first
* leading dimension is LDR1/2.
       CALL SFFTC3(-1,N1,N2,N3,ONE,V,LDR1,LDR2,V,LDR1/2,LDR2,TRIGS,
      $            IFAC,SW,LW,IERR)
       WRITE(*,*) 'in-place forward FFT of X:'
       CALL PRINT_REAL_AS_COMPLEX(N1/2+1, N2, N3, V, LDR1/2, LDR2)
* Compute 3-dimensional out-of-place inverse FFT. 
* First leading dimension of Z (LDR1) must be even
       CALL CFFTS3(1,N1,N2,N3,SCALE,Y,LDY1,LDY2,Z,LDR1,LDR2,TRIGS,
      $            IFAC,SW,0,IERR)
       WRITE(*,*) 'out-of-place inverse FFT of Y:'
       DO K = 1, N3
         DO I = 1, N1
            WRITE(*,'(5(F5.1,2X))') (Z(I,J,K), J = 1, N2)
         END DO
         WRITE(*,*)
       END DO
* Compute 3-dimensional in-place inverse FFT. 
* Y which is complex array containing input data is also
* used to store real results; as a real array, its first
* leading dimension is 2*LDY1.
       CALL CFFTS3(1,N1,N2,N3,SCALE,Y,LDY1,LDY2,Y,2*LDY1,LDY2,
      $            TRIGS,IFAC,SW,LW,IERR)
       WRITE(*,*) 'in-place inverse FFT of Y:'
       CALL PRINT_COMPLEX_AS_REAL(N1, N2, N3, Y, 2*LDY1, LDY2)
       DEALLOCATE(SW)
       END PROGRAM TESTSC3
       SUBROUTINE PRINT_COMPLEX_AS_REAL(N1, N2, N3, A, LD1, LD2)
       INTEGER N1, N2, N3, I, J, K
       REAL A(LD1, LD2, *)
       DO K = 1, N3
          DO I = 1, N1
             WRITE(*,'(5(F5.1,2X))') (A(I,J,K), J = 1, N2)
          END DO 
          WRITE(*,*)
       END DO
       END
       SUBROUTINE PRINT_REAL_AS_COMPLEX(N1, N2, N3, A, LD1, LD2)
       INTEGER N1, N2, N3, I, J, K
       COMPLEX A(LD1, LD2), *)
       DO K = 1, N3
          DO I = 1, N1
             WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))') ('(',REAL(A(I,J,K)),
      $              ',',AIMAG(A(I,J,K)),')', J = 1, N2)
          END DO
          WRITE(*,*)
       END DO
       END
my_system% f95 -dalign testsc3.f -xlibrary=sunperf
my_system% a.out
Three-dimensional complex-to-real and real-to-complex FFT
X =
0.1 0.4 0.7 1.0
0.2 0.5 0.8 1.1
0.3 0.6 0.9 1.2
4.1 3.4 2.7 1.0
1.2 6.5 4.8 3.1
2.3 1.6 7.9 2.2
out-of-place forward FFT of X:
Y =
( 48.6, 0.0) ( -9.6, -3.4) ( 3.4, 0.0) ( -9.6, 3.4)
( -4.2, -1.0) ( 2.5, -2.7) ( 1.0, 8.7) ( 9.5, -0.7)
(-33.0, 0.0) (  6.0, 7.0) ( -7.0,  0.0) (  6.0, -7.0)
(  3.0, 1.7) ( -2.5, 2.7) ( -1.0, -8.7) ( -9.5,  0.7)
in-place forward FFT of X:
( 48.6, 0.0) ( -9.6, -3.4) ( 3.4, 0.0) ( -9.6, 3.4)
( -4.2, -1.0) ( 2.5, -2.7) ( 1.0, 8.7) ( 9.5, -0.7)
(-33.0, 0.0) (  6.0, 7.0) ( -7.0, 0.0) (  6.0, -7.0)
(  3.0, 1.7) ( -2.5, 2.7) ( -1.0, -8.7) ( -9.5, 0.7)
out-of-place inverse FFT of Y:
0.1 0.4 0.7 1.0
0.2 0.5 0.8 1.1
0.3 0.6 0.9 1.2
4.1 3.4 2.7 1.0
1.2 6.5 4.8 3.1
2.3 1.6 7.9 2.2
in-place inverse FFT of Y:
0.1 0.4 0.7 1.0
0.2 0.5 0.8 1.1
0.3 0.6 0.9 1.2
4.1 3.4 2.7 1.0
1.2 6.5 4.8 3.1
2.3 1.6 7.9 2.2
 

Comments

When doing an in-place real-to-complex or complex-to-real transform, care must be taken to ensure the size of the input array is large enough to hold the results. For example, if the input is of type complex stored in a complex array with first leading dimension N, then to use the same array to store the real results, its first leading dimension as a real output array would be 2 × N. Conversely, if the input is of type real stored in a real array with first leading dimension 2 × N, then to use the same array to store the complex results, its first leading dimension as a complex output array would be N. Leading dimension requirements for in-place and out-of-place transforms can be found in Table 12, Table 13, and Table 14.

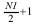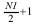In the linear and multi-dimensional FFT, the transform between real and complex data through a real-to-complex or complex-to-real transform can be confusing because N1 real data points correspond to complex data points. N1 real data points do map to N1 complex data points, but because there is conjugate symmetry in the complex data, only data points need to be stored as input in the complex-to-real transform and as output in the real-to-complex transform. In the multi-dimensional FFT, symmetry exists along all the dimensions, not just in the first. However, the two-dimensional and three-dimensional FFT routines store the complex data of the second and third dimensions in their entirety.

While the FFT routines accept any size of N1, N2 and N3, FFTs can be computed most efficiently when values of N1, N2 and N3 can be decomposed into relatively small primes. A real-to-complex or a complex-to-real transform can be computed most efficiently when

,

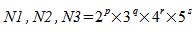and a complex-to-complex transform can be computed most efficiently when

,

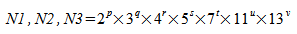where p, q, r, s, t, u, and v are integers and p, q, r, s, t, u, v ≥ 0.

The function xFFTOPT can be used to determine the optimal sequence length, as shown in Example 14. Given an input sequence length, the function returns an optimal length that is closest in size to the original length.

Example 14   RFFTOPT Example

my_system% cat fft_ex01.f
      PROGRAM TEST
      INTEGER         N, N1, N2, N3, RFFTOPT
C
      N = 1024
      N1 = 1019
      N2 = 71 
      N3 = 49
C
      PRINT *, 'N Original  N Suggested'
      PRINT '(I5, I12)', (N, RFFTOPT(N)) 
      PRINT '(I5, I12', (N1, RFFTOPT(N1)) 
      PRINT '(I5, I12)', (N2, RFFTOPT(N2)) 
      PRINT '(I5, I12)', (N3, RFFTOPT(N3)) 
      END
 
my_system% f95 -dalign fft_ex01.f -library=sunperf
my_system% a.out
 N Original  N Suggested
 1024        1024
 1019        1024
   71          72
   49          49
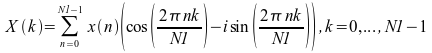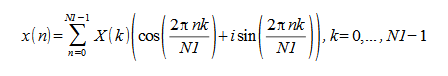
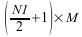