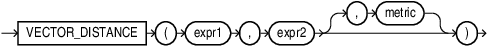1. Oracle AI Vector Search User's Guide
  2. Use SQL Functions for Vector Operations
  3. Vector Distance Functions and Operators
  4. VECTOR_DISTANCE

VECTOR_DISTANCE

VECTOR_DISTANCE is the main function that you can use to calculate the distance between two vectors.

Syntax


Description of vector_distance.eps follows
Description of the illustration vector_distance.eps

Purpose

VECTOR_DISTANCE takes two vectors as parameters. You can optionally specify a distance metric to calculate the distance. If you do not specify a distance metric, then the default distance metric is cosine. If the input vectors are BINARY vectors, the default metric is hamming.

You can optionally use the following shorthand vector distance functions:

  • L1_DISTANCE

  • L2_DISTANCE

  • COSINE_DISTANCE

  • INNER_PRODUCT

  • HAMMING_DISTANCE

  • JACCARD_DISTANCE

All the vector distance functions take two vectors as input and return the distance between them as a BINARY_DOUBLE.

Note the following caveats:

  • If you specify a metric as the third argument, then that metric is used.

  • If you do not specify a metric, then the following rules apply:

    • If there is a single column referenced in expr1 and expr2 as in: VECTOR_DISTANCE(vec1, :bind), and if there is a vector index defined on vec1, then the metric used when defining the vector index is used.

      If no vector index is defined on vec1, then the COSINE metric is used.

    • If there are multiple columns referenced in expr1 and expr2 as in: VECTOR_DISTANCE(vec1, vec2), or VECTOR_DISTANCE(vec1+vec2, :bind), then for all indexed columns, if their metrics used in the definitions of the indexes are the same, then that metric is used.

      On the other hand, if the indexed columns do not have a common metric, or none of the columns have an index defined, then the COSINE metric is used.

  • In a similarity search query, if expr1 or expr2 reference an indexed column and you specify a distance metric that conflicts with the metric specified in the vector index, then the vector index is not used and the metric you specified is used to perform an exact search.

  • Approximate (index-based) searches can be done if only one column is referenced by either expr1 or expr2, and this column has a vector index defined, and the metric that is specified in the vector_distance matches the metric used in the definition of the vector index.

Parameters

  • expr1 and expr2 must evaluate to vectors and have the same format and number of dimensions.

    If you use JACCARD_DISTANCE or the JACCARD metric, then expr1 and expr2 must evaluate to BINARY vectors.

  • This function returns NULL if either expr1 or expr2 is NULL.

  • metric must be one of the following tokens :

    • COSINE metric is the default metric. It calculates the cosine distance between two vectors.

    • DOT metric calculates the negated dot product of two vectors. The INNER_PRODUCT function calculates the dot product, as in the negation of this metric.

    • EUCLIDEAN metric, also known as L2 distance, calculates the Euclidean distance between two vectors.

    • EUCLIDEAN_SQUARED metric, also called L2_SQUARED, is the Euclidean distance without taking the square root.

    • HAMMING metric calculates the hamming distance between two vectors by counting the number dimensions that differ between the two vectors.

    • MANHATTAN metric, also known as L1 distance or taxicab distance, calculates the Manhattan distance between two vectors.

    • JACCARD metric calculates the Jaccard distance. The two vectors used in the query must be BINARY vectors.

Shorthand Operators for Distances

Syntax

  • expr1 <-> expr2

    <-> is the Euclidean distance operator: expr1 <-> expr2 is equivalent to L2_DISTANCE(expr1, expr2) or VECTOR_DISTANCE(expr1, expr2, EUCLIDEAN)

  • expr1 <=> expr2

    <=> is the cosine distance operator: expr1 <=> expr2 is equivalent to COSINE_DISTANCE(expr1, expr2) or VECTOR_DISTANCE(expr1, expr2, COSINE)

  • expr1 <#> expr2

    <#> is the negative dot product operator: expr1 <#> expr2 is equivalent to -1*INNER_PRODUCT(expr1, expr2) or VECTOR_DISTANCE(expr1, expr2, DOT)

Examples Using Shorthand Operators for Distances

 '[1, 2]' <-> '[0,1]'
v1 <-> '[' || '1,2,3' || ']' is equivalent to v1 <-> '[1, 2, 3]'
v1 <-> '[1,2]' is equivalent to L2_DISTANCE(v1, '[1,2]')
v1 <=> v2 is equivalent to COSINE_DISTANCE(v1, v2)
 v1 <#> v2 is equivalent to -1*INNER_PRODUCT(v1, v2)

Examples

VECTOR_DISTANCE with metric EUCLIDEAN is equivalent to L2_DISTANCE: 

VECTOR_DISTANCE(expr1, expr2, EUCLIDEAN);
L2_DISTANCE(expr1, expr2);

VECTOR_DISTANCE with metric COSINE is equivalent to COSINE_DISTANCE: 

VECTOR_DISTANCE(expr1, expr2, COSINE);
COSINE_DISTANCE(expr1, expr2);

VECTOR_DISTANCE with metric DOT is equivalent to -1 * INNER_PRODUCT: 

VECTOR_DISTANCE(expr1, expr2, DOT);
-1*INNER_PRODUCT(expr1, expr2);

VECTOR_DISTANCE with metric MANHATTAN is equivalent to L1_DISTANCE: 

VECTOR_DISTANCE(expr1, expr2, MANHATTAN);
L1_DISTANCE(expr1, expr2);

VECTOR_DISTANCE with metric HAMMING is equivalent to HAMMING_DISTANCE: 

VECTOR_DISTANCE(expr1, expr2, HAMMING);
HAMMING_DISTANCE(expr1, expr2);

VECTOR_DISTANCE with metric JACCARD is equivalent to JACCARD_DISTANCE: 

VECTOR_DISTANCE(expr1, expr2, JACCARD);
JACCARD_DISTANCE(expr1, expr2);

Parent topic: Vector Distance Functions and Operators