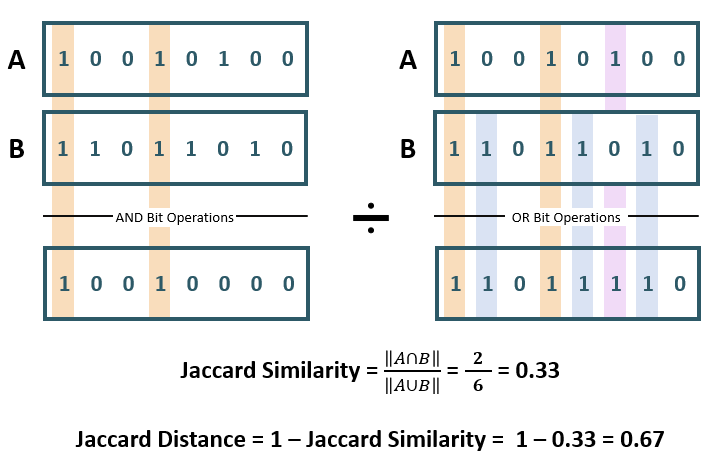
Jaccard Similarity
The Jaccard similarity is used to determine the share of significant
(non-zero) dimensions (bit's position) common between two BINARY
vectors.
The Jaccard similarity is only applicable to BINARY vectors and
only the non-zero bits of each vector are considered.
The Jaccard similarity between vectors A and B is the calculation
of the Hamming weight (norm, or the number of '1's in the resulting vector)
of the result of an AND bit operation between A and
B, divided by the Hamming weight of the result of an
OR bit operation between A and B.
As shown in the included diagram of vectors A and B:
- The
ANDbit operation outputs a 1 if the bits in the sequence match a 1, and 0 otherwise. - The
ORbit operation outputs a 1 if at least one of the bits in the sequence matches a 1, and 0 otherwise.
The result of the calculation is from 0 to 1, where results approaching 1 are more similar. A result of 0 means that the two vectors share no non-zero attributes while a result of 1 indicates the two vectors share identical sets of non-zero attributes. In the included diagram, the two vectors share 33% of the significant attributes.
While the Jaccard similarity indicates how similar two vectors are, the Jaccard distance indicates the dissimilarity between the vectors. The Jaccard distance can be found by subtracting the Jaccard similarity from 1. For example, two vectors with a Jaccard similarity of 0.25 have a Jaccard distance of 0.75. When determining distance, the meaning of the result is opposite to that of a similarity calculation. A result of 0 indicates that the two vectors are identical while a result of 1 indicates the vectors are completely disjoint, sharing no common elements.
Parent topic: Vector Distance Metrics