Addition

Vector addition is often used in Natural Language Processing (NLP) where words are often represented as vectors that capture their meaning in a numerical format. Vector addition is used to combine these meanings and understand relationships between words, a task also referred to as word analogy.

Given two vectors A=(a1, a2, a3) and B=(b1, b2, b3), C = A + B is computed as C = (a1+b1, a2+b2, a3+b3).

Subtraction

Vector subtraction can be used in word analogy scenarios but is also useful in the context of facial recognition. Each face can be represented by a vector of facial features (distance between eyes, eye color, and so on). Subtracting one vector from another gives you the main differences between the two faces, giving you the information needed to recognize whether they are similar or not.

Given two vectors A=(a1, a2, a3) and B=(b1, b2, b3), C = A - B is computed as C = (a1-b1, a2-b2, a3-b3).

Multiplication

Vector multiplication of each corresponding coordinate of two vectors, or element-wise product, is called the Hadamard product. The Hadamard product is often used in neural networks and computer vision.

Given two vectors A=(a1, a2, a3) and B=(b1, b2, b3), the Hadamard product A*B is computed as A*B = (a1*b1, a2*b2, a3*b3).

Semantics

Both sides of the operation must evaluate to vectors with matching dimensions and must not be BINARY or SPARSE vectors. The resulting vector has the same number of dimensions as the operands and the format is determined based on the formats of the inputs. If one side of the operation is not a vector, an attempt is made automatically to convert the value to a vector. If the conversion fails, an error is raised.

The format used for the result is ranked in the following order: flexible, FLOAT64, FLOAT32, then INT8. As in, if either side of the operation has a flexible format, the result will be flexible, otherwise, if either side has the format FLOAT64, the result will be FLOAT64, and so on.

Consider two vectors with the following values:

v1 = [1, 2, 3]
v2 = [10, 20, 30]

If either side of the arithmetic operation is NULL, the result is NULL. In the case of dimension overflow, an error is raised. For example, adding VECTOR('[1, 127]', 2, INT8) to VECTOR('[1, 1]', 2, INT8) results in an error because 127+1=128, which overflows the INT8 format.

The use of division operators on vectors is not supported.

Examples

Word Analogy

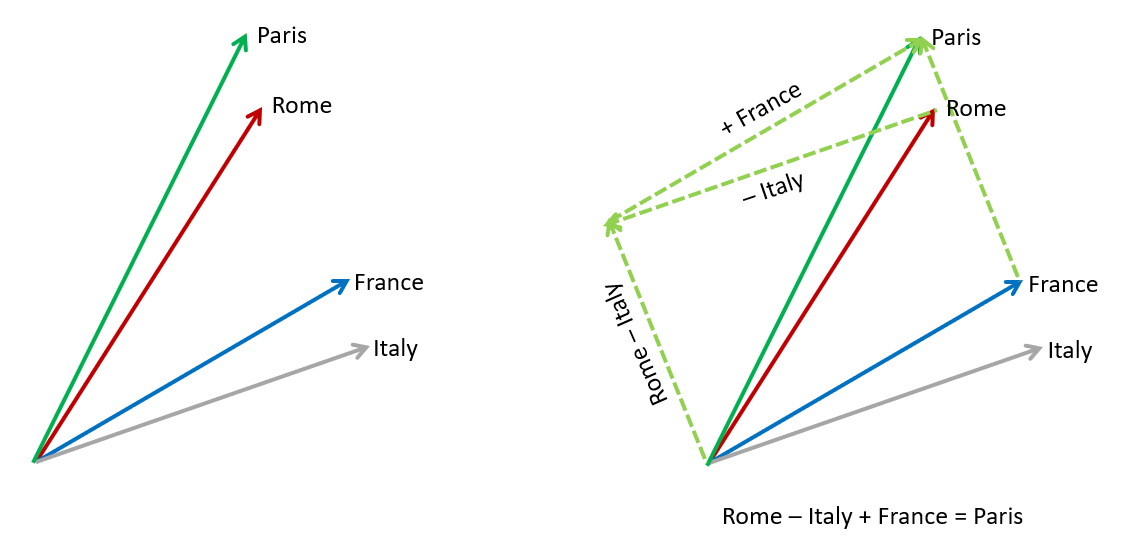
Using word embeddings, suppose you want to find the relationship between "Rome" and "Paris". You can take the vector for "Rome", subtract the vector for "Italy", and then add the vector for "France". This results in a new vector that approximates the meaning of the word "Paris". The calculation should be "Rome - Italy + France = Paris" using an ideal embedding model.

Basic Vector Arithmetic

SELECT VECTOR('[5, 10, 15]') - VECTOR('[2, 4, 6]');

VECTOR('[5,10,15]')-VECTOR('[2,4,6]')
------------------------------------------------------------
[3.0E+000,6.0E+000,9.0E+000]


SELECT VECTOR('[1, 2, 3]', 3, FLOAT64) + VECTOR('[4, 5, 6]', 3, FLOAT32) * '[2, 2, 2]';

VECTOR('[1,2,3]',3,FLOAT64)+VECTOR('[4,5,6]',3,FLOAT32)*'[2,2,2]'
--------------------------------------------------------------------------------
[9.0E+000,1.2E+001,1.5E+001]

DECLARE
  v1 VECTOR := VECTOR('[10, 20, 30]', 3, INT8);
  v2 VECTOR := VECTOR('[6, 4, 2]', 3, INT8);
BEGIN
  DBMS_OUTPUT.PUT_LINE(TO_CHAR(v1 + v2));
  DBMS_OUTPUT.PUT_LINE(TO_CHAR(v1 - v2));
  DBMS_OUTPUT.PUT_LINE(TO_CHAR(v1 * v2));
END;  
/

Result:

[16,24,32]
[4,16,28]
[60,80,60]