Information about Model settings

Evaluate the model by examining the various statistics generated after building the model. The statistics indicate the model's quality.

• Run the following script for model details available through the Random Forest model object, like the model settings, coefficients, fit details, etc.

  rf_mod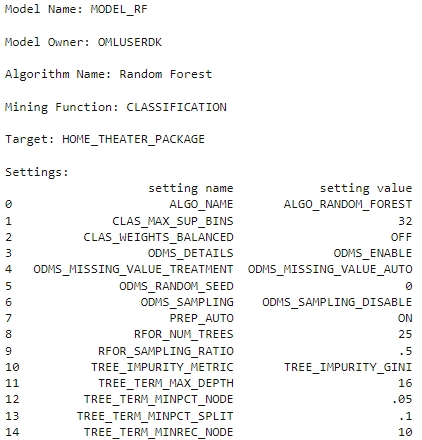

  
  
  
  
  

  They can also be displayed and viewed individually as shown below.

• Run the following script to display the model's global statistics.

  z.show(rf_mod.global_stats)

  
  
  
  
  
• Run the following script to display the attribute importance of the rf_mod model.

  z.show(rf_mod.importance)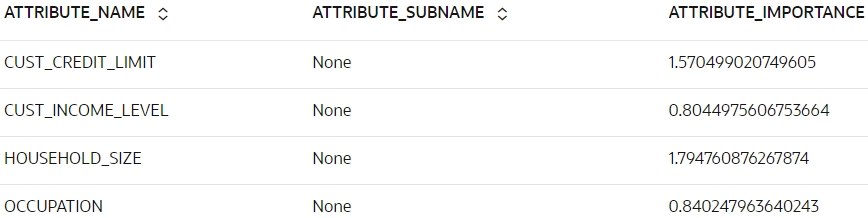

  
  
  
  
  

Score

Here you will make predictions on the test case using the model and then evaluate the model by using methods like Confusion Matrix, Lift Chart, Gains Chart, and ROC curve chart.

1. Make predictions on the test data and add the CASE_ID as a supplemental column so you can uniquely associate scores with the original data. To do so run the below script:

   # Set the case ID attribute
   case_id = 'CUST_ID'
   # Gather the Predictions
   RES_DF = rf_mod.predict(TEST_X, supplemental_cols = TEST_X)
   # Additionally collect the PROBABILITY_OF_0 and PROBABILITY_OF_1
   RES_PROB = rf_mod.predict_proba(TEST_X, supplemental_cols = TEST_X[case_id])
   # Join the entire result into RES_DF
   RES_DF = RES_DF.merge(RES_PROB, how = "inner", on = case_id, suffixes = ["", ""])
   

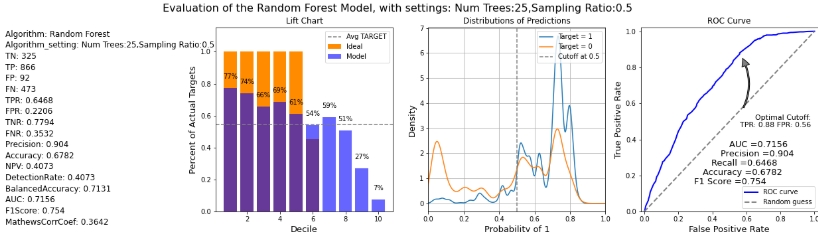
2. To evaluate the model, pass a proxy object oml.Dataframe containing predictions and the target columns in a user-defined function named evaluate_model. Evaluate your model using standard metrics. For a classification example, you can evaluate your model using the following:

   • Confusion Matrix: It displays the number and type of correct and incorrect predictions made with respect to the actual classification in the test data. It is an n-by-n matrix where n is the number of classes.
   • Lift Chart: Applies only to binary classification requiring the designation of the positive class. It measures the degree to which the predictions of a classification model are better than randomly generated predictions.
   • ROC curve chart: Applies to binary classification and requires the designation of the positive class. These are metrics for comparing predicted and actual target values in a classification model.

   Run the below script to generate the metrics and charts:

   def evaluate_model(pred_data='', settings_name={''}, name='', target=''):
       """Evaluate the models by passing an proxy oml.Dataframe containing Predictions
       and the target column,
       The Settings name (for the charts), 
       The name of the model used (for the charts),
       Supply the target column name for evaluation
       for computing the confusion matrix with the test dataset"""
       import oml
       import numpy as np
       import matplotlib.pyplot as plt
       from sklearn.metrics import auc
       from sklearn.metrics import roc_curve
   
       conf_matrix = pred_data.crosstab(target,'PREDICTION',pivot=True)
   
       # Extract Statistics from the Confusion Matrix
       cf_local = conf_matrix.pull()
       TN = int(cf_local[cf_local[target]==0]['count_(0)'])
       FN = int(cf_local[cf_local[target]==0]['count_(1)'])
       TP = int(cf_local[cf_local[target]==1]['count_(1)'])
       FP = int(cf_local[cf_local[target]==1]['count_(0)'])
       TPR = TP/(TP+FN)
       FPR = FP/(FP+TN)
       TNR = TN/(TN+FP)
       FNR = FN/(FN+TP)
       Precision = TP/(TP+FP)
       Accuracy = (TP+TN)/(TP+TN+FP+FN)
       NPV = TN/(FN+TN)
       DetectionRate = TN/(FN+TN)
       BalancedAccuracy = (TPR+TNR)/2
   
       # Estimated AUC via Triangle (not very precise) could be
       # AUC = (1/2)*FPR*TPR + (1/2)*(1-FPR)*(1-TPR) + (1-FPR)*TPR
       # Compute real AUC using roc_curve by loading the
       # data locally and using the roc_curve() function
       pred_local = pred_data.pull()
       fpr, tpr, _ = roc_curve(pred_local[[target]],pred_local[['PROBABILITY_OF_1']])
       AUC = auc(fpr, tpr)
       opt_index = np.argmax(tpr - fpr)
       FPR_OPT = fpr[opt_index]
       TPR_OPT = tpr[opt_index]
       F1Score = 2*Precision*TPR/(Precision+TPR)
       MathewsCorrCoef = ((TP*TN)-(FP*FN))/((TP+FP)*(TP+FN)*(TN+FP)*(TN+FN))**0.5
   
       # Store all statistics to export
       statistics = {'Algorithm' : name,
                   'Algorithm_setting' : settings_name,
                   'TN' : TN,
                   'TP' : TP,
                   'FP' : FP,
                   'FN' : FN,
                   'TPR' : TPR,
                   'FPR' : FPR,
                   'TNR' : TNR,
                   'FNR' : FNR,
                   'Precision' : Precision,
                   'Accuracy' : Accuracy,
                   'NPV' : NPV,
                   'DetectionRate' : DetectionRate,
                   'BalancedAccuracy' : BalancedAccuracy,
                   'AUC' : AUC,
                   'F1Score' : F1Score,
                   'MathewsCorrCoef' : MathewsCorrCoef
                   }
       # Nice round stats for printing to screen
       TOTAL = TP+TN+FP+FN
       TN_P = round((TN/TOTAL*100),2)
       FP_P = round((FP/TOTAL*100),2)
       FN_P = round((FN/TOTAL*100),2)
       TP_P = round((TP/TOTAL*100),2)
       # Print the output nicely on Zeppelin native Table
       print("%table CONFUSION MATRIX\tPREDICTED 0\tPREDICTED 1\nACTUAL 0\t"+
           "True Negative: "+str(TN)+" ("+str(TN_P)+"%)\t"+
           "False Positive: "+str(FP)+" ("+str(FP_P)+"%)\nACTUAL 1\t"+
           "False Negative: "+str(FN)+" ("+str(FN_P)+"%)\t"+
           "True Positive: "+str(TP)+" ("+str(TP_P)+"%)\n"+
           "Accuracy: "+str(round(Accuracy*100,4))+"%\t"+
           "AUC: "+str(round(AUC,4))+"\t"+
           "F1Score: "+str(round(F1Score,4))
           )
   
       # Multiple Charts for Evaluation
       fig, axes = plt.subplots(nrows=1, ncols=4,figsize=[22,5])
       ax1, ax2, ax3, ax4 = axes.flatten()
       fig.suptitle('Evaluation of the '+str(name)+' Model, with settings: '+str(settings_name), size=16)
   
       # Statistics
       ax1.axis('off')
   
       # Function to return rounded numbers if the string is float, return
       # integers otherwise and return characters if not a number
       def round_if_float(content):
           try:
               val = float(content)
           except ValueError:
               return(content)
           else:
               if val.is_integer():
                   return(int(content))
               else:
                   return(round(float(content),4))
   
       for num, name in enumerate(statistics):
           ax1.text(0.01, 
           (-num*0.06+0.94),
           "{0}: {1}".format(name,round_if_float(statistics[name])),
           ha='left', 
           va='bottom', 
           fontsize=12)
   
       # Produce Lift Chart
       ax2.set_title('Lift Chart')
       data = pred_local.sort_values(by='PROBABILITY_OF_1', ascending=False)
       data['row_id'] = range(0,0+len(data))
       data['decile'] = ( data['row_id'] / (len(data)/10) ).astype(int)
       lift = data.groupby('decile')[target].agg(['count','sum'])
       lift.columns = ['count', target]
       lift['decile'] = range(1,11)
   
       data_ideal = pred_local.sort_values(by=target, ascending=False)
       data_ideal['row_id'] = range(0,0+len(data))
       data_ideal['decile'] = ( data_ideal['row_id'] / (len(data_ideal)/10) ).astype(int)
       lift_ideal = data_ideal.groupby('decile')[target].agg(['count','sum'])
       lift_ideal.columns = ['count', 'IDEAL']
       lift['IDEAL']=lift_ideal['IDEAL']
   
       ax2.bar(lift['decile'],lift['IDEAL']/lift['count'],
       color='darkorange', label='Ideal')
       ax2.bar(lift['decile'],lift[target]/lift['count'],
       color='blue', alpha=0.6, label='Model')
       ax2.axhline((lift[target]/lift['count']).mean(), 
       color='grey', linestyle='--', label='Avg TARGET')
       ax2.set_ylim(0,1.15)
       ax2.set_xlabel('Decile', size=13)
       ax2.set_ylabel('Percent of Actual Targets', size=13)
       # Print labels.
       for dec in lift['decile']:
           ax2.text(dec, lift[lift.decile==dec][target]/lift[lift.decile==dec]['count'] + 0.05, 
           ("%.0f" % int(round((lift[(lift.decile==dec)][target]/lift[lift.decile==dec]['count'])*100,0)))+"%",
           ha='center', va='bottom')
       ax2.legend(loc="upper right")
   
       # Produce Gains Chart
       ax3.set_title('Distributions of Predictions')
       pred_local[pred_local[target]==1]['PROBABILITY_OF_1'].rename("Target = 1").plot(kind='density', bw_method=0.1, grid=True, ax=ax3)
       pred_local[pred_local[target]==0]['PROBABILITY_OF_1'].rename("Target = 0").plot(kind='density', bw_method=0.1, grid=True, ax=ax3)
       ax3.axvline(.5, color='grey', linestyle='--', label='Cutoff at 0.5')
       ax3.set_xlim([0,1])
       ax3.set_xlabel('Probability of 1', size=13)
       ax3.set_ylabel('Density', size=13)
       ax3.legend(loc="upper right")
   
       # ROC curve Chart
       ax4.set_title('ROC Curve')
       ax4.plot(fpr, tpr, color='blue', lw=2, label='ROC curve')
       ax4.plot(FPR_OPT, TPR_OPT,  color='orange', markersize=6)
       ax4.plot([0, 1], [0, 1], lw=2, linestyle='--', color='grey', label='Random guess')
       ax4.annotate('Optimal Cutoff:\nTPR: '+str(round(TPR_OPT,2))+' FPR: '+str(round(FPR_OPT,2)),
                   fontsize=11, xy=(FPR_OPT, TPR_OPT), xycoords='data', xytext=(0.98, 0.54), 
                   textcoords='data', 
                   arrowprops=dict(facecolor='gray', shrink=0.1, width=2,
                                   connectionstyle='arc3, rad=0.3'), 
                   horizontalalignment='right', verticalalignment='top')
       ax4.annotate('AUC ='+str(round(AUC,4)), xy=(0.5, 0.35), 
                   xycoords='axes fraction', size=13)
       ax4.annotate('Precision ='+str(round(Precision,4)), xy=(0.45, 0.3), 
                   xycoords='axes fraction', size=13)
       ax4.annotate('Recall ='+str(round(TPR,4)), xy=(0.4, 0.25), 
                   xycoords='axes fraction', size=13)
       ax4.annotate('Accuracy ='+str(round(Accuracy,4)), xy=(0.35, 0.2),
                   xycoords='axes fraction', size=13)
       ax4.annotate('F1 Score ='+str(round(F1Score,4)), xy=(0.3, 0.15), 
                   xycoords='axes fraction', size=13)
       ax4.set_xlim([-0.02, 1.02])
       ax4.set_ylim([0.0, 1.02])
       ax4.set_xlabel('False Positive Rate', size=13)
       ax4.set_ylabel('True Positive Rate', size=13) 
       ax4.legend(loc="lower right")
   
       return(statistics, pred_local)
       
   _ = evaluate_model(pred_data=RES_DF, settings_name='Num Trees:25,Sampling Ratio:0.5', name='Random Forest', target='HOME_THEATER_PACKAGE')

   
   
   
   
   
   
   
   
   
3. Display the results of customers responding to HOME_THEATER_PACKAGE with a probability greater than 0.5. Select the columns from the RES_DF dataset to display. To do so, run the following script:

   z.show(RES_DF[RES_DF['PROBABILITY_OF_1'] > 0.5])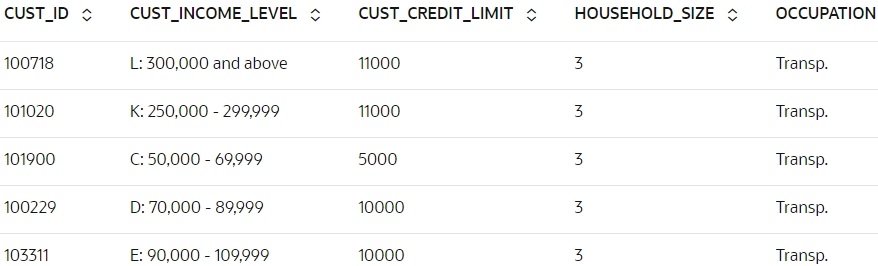

   
   
   
   
   
4. Run the following script to get the model accuracy of the rf_mod. The score function makes prediction on the Test data and the target test data and gives the mean accuracy.

   print("RF accuracy score = {:.2f}".format(rf_mod.score(TEST_X, TEST_Y)))

   RF accuracy score = 0.68

   You obtain an accuracy of 0.68 or approximately 68% of the result are correctly predicted.

To conclude, you have successfully identified customers who are likely to purchase HOME_THEATER_PACKAGE. This prediction helps to promote and offer home theater package to the target customers.