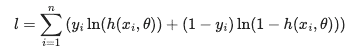GWR Classifier
The Geographically Weighted Regression (GWR) classifier is a binary classifier used in the presence of spatial heterogeneity, which can be identified as a sign of regional variation.
The algorithm creates a local classifier for every observation in the dataset by incorporating the target and explanatory variables from the observations within their neighborhood, allowing the relationships between the independent and dependent variables to vary by locality.
The classifier trains a logistic regression model for every sample in the dataset, incorporating the dependent and independent variables of locations falling within a specified bandwidth. The goal is to maximize the cross-entropy loss function defined as follows.
In the preceding function, y is either 0 or
1, the function h is the activation function for Logistic
Regression, which is the Sigmoid function.
The following table describes the main methods of the
GWRClassifier class.
| Method | Description |
|---|---|
fit |
The algorithm requires a bandwidth, which can be set by
the user with the bandwidth parameter or by specifying
the spatial_weights_definition parameter.
If the
If neither the
|
predict |
To make predictions, GWR trains a model for each observation on the prediction set using neighboring observations from the training data. Then, it uses those models to estimate the target variable. |
fit_predict |
Calls the fit and
predict methods sequentially with the training
data.
|
score |
Returns the model's accuracy for the given data. |
See the GWRClassifier class in Python API Reference for Oracle Spatial AI for more information.
The following example uses the block_groups
SpatialDataFrame and performs the following steps:
- Creates a categorical variable based on the
MEDIAN_INCOMEcolumn to be used as the target variable. - Creates an instance of
GWRClassifier. - Trains the model using a training set.
- Prints the predictions from the model and the model's accuracy using the trained model.
import pandas as pd
from oraclesai.preprocessing import spatial_train_test_split
from oraclesai.weights import DistanceBandWeightsDefinition
from oraclesai.classification import GWRClassifier
from oraclesai.pipeline import SpatialPipeline
from sklearn.preprocessing import StandardScaler
# Create a categorical variable, "INCOME_LABEL", based on the second quantile of the median income
block_groups_extended = block_groups.add_column("INCOME_LABEL", pd.qcut(block_groups['MEDIAN_INCOME'].values, [0, 0.5, 1], labels=[0, 1]).to_list())
# Set a referenced coordinate system
block_groups_extended = block_groups_extended.to_crs('epsg:3857')
# Define the target and explanatory variables
X = block_groups_extended[['INCOME_LABEL', 'MEAN_AGE', 'MEAN_EDUCATION_LEVEL', 'HOUSE_VALUE', 'INTERNET', 'geometry']]
# Define the training and test sets
X_train, X_test, _, _, _, _ = spatial_train_test_split(X, y="median_income", test_size=0.2, random_state=32)
# Define the spatial weights definition
weights_definition = DistanceBandWeightsDefinition(threshold=15000)
# Create an instance of GWRClassifier
gwr_classifier = GWRClassifier(spatial_weights_definition=weights_definition)
# Add the model to a spatial pipeline along with a pre-processing step
classifier_pipeline = SpatialPipeline([('scale', StandardScaler()), ('gwr', gwr_classifier)])
# Train the model specifying the target variable
classifier_pipeline.fit(X_train, "INCOME_LABEL")
# Print the predictions with the test set
gwr_predictions_test = classifier_pipeline.predict(X_test.drop("INCOME_LABEL")).flatten()
print(f"\n>> predictions (X_test):\n {gwr_predictions_test[:10]}")
# Print the accuracy with the test set
gwr_accuracy_test = classifier_pipeline.score(X_test, "INCOME_LABEL")
print(f"\n>> accuracy (X_test):\n {gwr_accuracy_test}")The output consists of the predictions of the first 10 observations and the model's accuracy using the test set.
>> predictions (X_test):
[1 1 0 0 1 0 1 0 0 0]
>> accuracy (X_test):
0.8384279475982532The summary property includes statistics of a global
logistic regression and the GWRClassifier. As for the estimated
parameters, it displays the average value from all the local models.
===========================================================================
Model type Binomial
Number of observations: 2750
Number of covariates: 5
Global Regression Results
---------------------------------------------------------------------------
Deviance: 2088.938
Log-likelihood: -1044.469
AIC: 2098.938
AICc: 2098.960
BIC: -19649.694
Percent deviance explained: 0.452
Adj. percent deviance explained: 0.451
Variable Est. SE t(Est/SE) p-value
------------------------------- ---------- ---------- ---------- ----------
X0 -0.044 0.061 -0.717 0.473
X1 0.439 0.072 6.084 0.000
X2 0.685 0.104 6.603 0.000
X3 0.542 0.109 4.989 0.000
X4 1.298 0.092 14.088 0.000
Geographically Weighted Regression (GWR) Results
---------------------------------------------------------------------------
Spatial kernel: Fixed bisquare
Bandwidth used: 15000.000
Diagnostic information
---------------------------------------------------------------------------
Effective number of parameters (trace(S)): 56.675
Degree of freedom (n - trace(S)): 2693.325
Log-likelihood: -888.994
AIC: 1891.337
AICc: 1893.765
BIC: 2226.816
Percent deviance explained: 0.534
Adjusted percent deviance explained: 0.524
Adj. alpha (95%): 0.004
Adj. critical t value (95%): 2.850
Summary Statistics For GWR Parameter Estimates
---------------------------------------------------------------------------
Variable Mean STD Min Median Max
-------------------- ---------- ---------- ---------- ---------- ----------
X0 -0.020 0.846 -1.630 -0.140 3.328
X1 0.512 0.325 0.020 0.385 2.156
X2 0.931 0.665 -1.213 1.168 2.893
X3 0.995 0.981 -0.615 0.834 6.249
X4 1.190 0.356 0.324 1.119 2.531
===========================================================================