The global spatial autocorrelation is a way to measure the overall trend followed by the values of a certain variable across different locations.

The Moran’s I statistic is a common way to calculate the global spatial autocorrelation and is defined by the following formula.

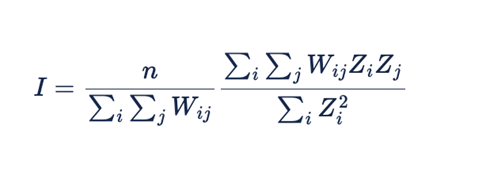
Description of the illustration spatial_ai_autocorrelation_formula.png

In the preceding formula, n is the number of observations, W is the spatial weights matrix, and Z is the standardized variable of interest.

A positive value of Moran’s I statistic indicates the presence of clusters where similar values tend to be together, reflecting the effect of spatial dependence. In contrast, a negative value of Moran’s I statistic suggests the presence of a checkerboard pattern or spatial variance where neighboring observations have dissimilar values, reflecting the effect of spatial heterogeneity.

Oracle Spatial AI provides the MoranITest.create function as part of oraclesai.analysis, which calculates the Moran’s I statistic for a given variable of a dataset.

See the MoranITest class in Python API Reference for Oracle Spatial AI for more information.

The following code uses the MoranITest.create function to calculate the Moran’s I statistic of the MEDIAN_INCOME column from the SpatialDataFrame block_groups. The class uses spatial weights to obtain the values from neighboring locations, which must be passed as a parameter, along with the dataset and the column of interest.

from oraclesai.analysis import MoranITest
from oraclesai.weights import SpatialWeights, KNNWeightsDefinition

spatial_weights = SpatialWeights.create(block_groups["geometry"].values, KNNWeightsDefinition(k=5))  

moran_test = MoranITest.create(block_groups, spatial_weights, column_name="MEDIAN_INCOME")

print(f"Moran's I = {moran_test.i}")
print(f"p-value = {moran_test.p_value}")

The preceding code prints the Moran’s I statistic and its p-value. The positive value of the statistic indicates the presence of clustering where locations of similar income tend to be together.

Moran's I = 0.652331479721869
p-value = 0.001