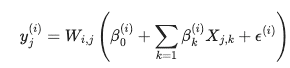Geographically Weighted Regression
The Geographically Weighted Regression (GWR) model is used in the presence of spatial heterogeneity, which can be identified as a sign of regional variation.
The GWR model creates a local linear regression model for every observation in the dataset. It incorporates the target and explanatory variables from the observations within their neighborhood, allowing the relationships between the independent and dependent variables to vary by locality.
The following shows the equation for the GWR model:
In the preceding equation, W is the spatial weights
matrix, yj(i) is the estimation of the
target variable for observation j at location
i .
The GWRRegressor class trains local linear regressions for every sample
in the dataset, incorporating the dependent and independent variables of locations
falling within a specified bandwidth.
The following table describes the main methods of the
GWRRegressor class.
| Method | Description |
|---|---|
fit |
The algorithm requires a bandwidth, which can be set by
the user with the bandwidth parameter or by specifying
the spatial_weights_definition parameter.
If the
bandwidth nor the
spatial_weights_definition parameters are defined,
then the bandwidth is estimated internally based on the
geometries.
|
predict |
To make predictions, GWR creates a model for each observation on the prediction set using neighboring observations from the training data. Then, it uses those models to estimate the target variable. |
fit_predict |
Calls the fit and
predict methods sequentially with the training
data.
|
score |
Returns the R-squared statistic for the given data. |
See the GWRRegressor class in Python API Reference for Oracle Spatial AI for more information.
The following example uses the block_groups
SpatialDataFrame and the GWRRegressor to train a
model to predict the target variable, MEDIAN_INCOME. It uses a training
set to train the model and a test set to make predictions of the target variable and
obtain the R-squared statistic.
from oraclesai.preprocessing import spatial_train_test_split
from oraclesai.weights import DistanceBandWeightsDefinition
from oraclesai.regression import GWRRegressor
from oraclesai.pipeline import SpatialPipeline
from sklearn.preprocessing import StandardScaler
# Define target and explanatory variables
X = block_groups[['MEDIAN_INCOME', 'MEAN_AGE', 'MEAN_EDUCATION_LEVEL', 'HOUSE_VALUE', 'INTERNET', 'geometry']]
# Use a referenced coordinate system
X = X.to_crs("epsg:3857")
# Define training and test sets
X_train, X_test, _, _, _, _ = spatial_train_test_split(X, y="MEDIAN_INCOME", test_size=0.1, random_state=32)
# Define the spatial weights
weights_definition = DistanceBandWeightsDefinition(threshold=10000)
# Create an instance of GWR passing the spatial weights
gwr_model = GWRRegressor(spatial_weights_definition=weights_definition)
# Add the regressor to a pipeline along with a preprocessing step
gwr_pipeline = SpatialPipeline([('scale', StandardScaler()), ('gwr_regression', gwr_model)])
# Train the model specifying the target variable
gwr_pipeline.fit(X_train, "MEDIAN_INCOME")
# Print the predictions with the test set
gwr_predictions_test = gwr_pipeline.predict(X_test.drop(["MEDIAN_INCOME"])).flatten()
print(f"\n>> predictions (X_test):\n {gwr_predictions_test[:10]}")
# Print the score with the test set
gwr_r2_score = gwr_pipeline.score(X_test, y="MEDIAN_INCOME")
print(f"\n>> r2_score (X_test):\n {gwr_r2_score}")The output of the program is shown is as shown:
>> predictions (X_test):
[111751.58871802 123406.64795915 25850.4248602 23565.60954771
180171.51825151 47052.37667604 118800.80714934 31067.07113894
62079.81316461 30673.82128591]
>> r2_score (X_test):
0.6942389040067138The summary property includes statistics of the OLS and GWR
models. As for the estimated parameters, it displays the average value from all the
local models.
===========================================================================
Model type Gaussian
Number of observations: 3093
Number of covariates: 5
Global Regression Results
---------------------------------------------------------------------------
Residual sum of squares: 1816309978579.363
Log-likelihood: -35614.052
AIC: 71238.104
AICc: 71240.132
BIC: 1816309953761.425
R2: 0.635
Adj. R2: 0.634
Variable Est. SE t(Est/SE) p-value
------------------------------- ---------- ---------- ---------- ----------
X0 69761.518 436.080 159.974 0.000
X1 2555.817 564.452 4.528 0.000
X2 5613.607 843.158 6.658 0.000
X3 19204.921 602.745 31.862 0.000
X4 10031.929 637.215 15.743 0.000
Geographically Weighted Regression (GWR) Results
---------------------------------------------------------------------------
Spatial kernel: Fixed bisquare
Bandwidth used: 10000.000
Diagnostic information
---------------------------------------------------------------------------
Residual sum of squares: 1247690194588.343
Effective number of parameters (trace(S)): 117.770
Degree of freedom (n - trace(S)): 2975.230
Sigma estimate: 20478.262
Log-likelihood: -35033.321
AIC: 70304.183
AICc: 70313.751
BIC: 71021.184
R2: 0.749
Adjusted R2: 0.739
Adj. alpha (95%): 0.002
Adj. critical t value (95%): 3.075
Summary Statistics For GWR Parameter Estimates
---------------------------------------------------------------------------
Variable Mean STD Min Median Max
-------------------- ---------- ---------- ---------- ---------- ----------
X0 62341.157 12808.790 -66225.562 64262.819 94371.705
X1 2998.233 3153.236 -12716.566 3338.876 18130.392
X2 10539.611 7148.106 -7226.756 9336.382 70067.037
X3 16577.403 9934.050 -9579.528 16819.683 47874.385
X4 9771.744 4232.729 1656.213 9326.487 44417.212
===========================================================================