Explore the Data
Exploring the data helps you to understand the variables individually and how they interact.
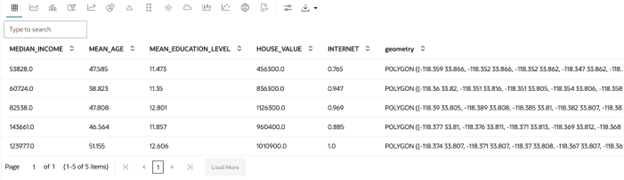
Perform the following steps to explore the data:- Understand the data by visualizing the first five observations of the training
set using the
headmethod.from oraclesai import enable_geodataframes enable_geodataframes(z) z.show(X_train.head())The output is as shown:
- Define spatial weights to understand the influence of each variable in
neighboring locations (by establishing the relationship between neighboring
locations).
Use the K-Nearest Neighbor approach, which indicates that for each observation, the nearest K observations are considered neighbors.
from oraclesai.weights import KNNWeightsDefinition weights_definition = KNNWeightsDefinition(k=10) - Calculate the spatial lag to study the interaction with the neighboring
locations.
The spatial lag of an observation represents the average value of a certain feature among its neighbors. For example, the average house value across neighboring locations.
The following code calculates the spatial lag for all the variables in the training set, except the geometries.
from oraclesai.preprocessing import SpatialLagTransformer X_spatial_lag = SpatialLagTransformer(weights_definition).fit_transform(X_train)According to Tobler's first law of geography, everything is related to everything else, but near things are more related than distant things. To understand the relation between features in a specific location, use the correlation between a feature and its spatial lag. For example, a strong positive correlation between the median income and the average income from neighboring locations could indicate an influence on the median income from its neighbors.
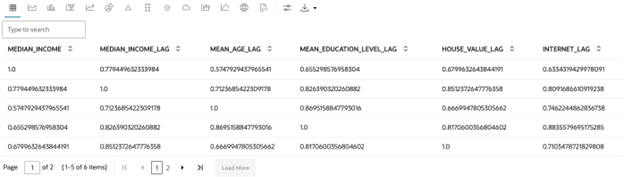
The following code displays the correlation matrix of the spatial lag variables and the target variable, where the spatial lag variables have the suffix
_LAG.import numpy as np import pandas as pd # Append the target variable to the spatial lag variables X_target_spatial_lag = np.append(X_train["MEDIAN_INCOME"].get_values(), X_spatial_lag, 1) # Create a Pandas' DataFrame columns = ["MEDIAN_INCOME", "MEDIAN_INCOME_LAG", "MEAN_AGE_LAG", "MEAN_EDUCATION_LEVEL_LAG", "HOUSE_VALUE_LAG", "INTERNET_LAG"] X_target_spatial_lag_df = pd.DataFrame(data=X_target_spatial_lag, columns=columns) z.show(X_target_spatial_lag_df.corr())The output is as shown:
- Measure the influence of neighbors.There is a strong positive correlation between the target variable (
MEDIAN_INCOME) and its spatial lag (MEDIAN_INCOME_LAG). This indicates that locations with similar income tend to be together, which is an indicator of spatial dependence.To confirm the presence of spatial dependence, calculate the Moran’s I statistic, which measures spatial autocorrelation.
- A positive and significant value indicates the presence of spatial clustering, where regions with similar values (high or low) tend to be together, reflecting the effect of spatial dependence.
- A negative and significant value indicates the presence of spatial variance or the checkerboard pattern, reflecting the effect of spatial heterogeneity.
from oraclesai.analysis import MoranITest from oraclesai.weights import SpatialWeights # Create spatial weights from definition spatial_weights = SpatialWeights.create(X_train["geometry"].values, weights_definition) # Run the Moran's I test moran_test = MoranITest.create(X_train, spatial_weights, column_name="MEDIAN_INCOME") # Print the Moran's I and the p-value print("Moran's I = ", moran_test.i) print("p_value = ", moran_test.p_value)The Moran’s I statistic is positive and significant, confirming the presence of spatial dependence in the target variable.
Moran's I = 0.5744827266749303 p_value = 0.001 - Get the spatial statistics.
Some spatial statistics become available by running the OLS model with spatial diagnostics. To get spatial diagnostics, it is required to define the spatial weights when creating the instance of
OLSRegressor.from oraclesai.regression import OLSRegressor ols_model = OLSRegressor(weights_definition).fit(X_train, "MEDIAN_INCOME")Obtain the Moran’s I statistic from the model’s residuals using the
moran_res metricfromoraclesai.metrics.from oraclesai.metrics import moran_res morans_i, _, p_value = moran_res(ols_model) print(f"Moran's I = {morans_i}") print(f"p_value = {p_value}")The positive and significant value of Moran’s I statistic of the residuals indicates the presence of spatial dependence in the residuals, which means that the prediction error of an observation is similar to the prediction error of its neighbors.
Moran's I = 0.2594180201084295 p_value = 9.432690077796932e-203The two regression models , Spatial Lag Model and Spatial Error Model, include the effect of spatial dependence in their regression equation.
Use the Lagrange Multipliers tests from the spatial diagnostics of the trained OLS model to choose the best model for the data. The Lagrange Multiplier tests for Spatial Lag and Spatial Error are part of
oraclesai.metrics.from oraclesai.metrics import lm_lag, lm_error, rlm_lag, rlm_error print(f"Lagrange Multiplier (lag): {lm_lag(ols_model)}") print(f"Robust LM (lag): {rlm_lag(ols_model)}") print(f"Lagrange Multiplier (error): {lm_error(ols_model)}") print(f"Robust LM (error): {rlm_error(ols_model)}")Use the robust tests when Lagrange Multiplier tests are significant for Spatial Lag and Spatial Error. Both robust tests are significant, but the value of the statistic for spatial error is much larger, indicating that the Spatial Error model is a better fit for the data.
Lagrange Multiplier (lag): (357.8764476978743, 8.165543828650201e-80) Robust LM (lag): (10.656323334376838, 0.001096952308135397) Lagrange Multiplier (error): (904.2345462924114, 1.178375337257614e-198) Robust LM (error): (557.0144219289139, 3.750470342578867e-123)