The AdaptiveSpatialRegressor class consists of an automated approach that finds the regression algorithm that better fits the data. This is the best approach when you do not know which model to use.

The algorithm trains an OLSRegressor model specifying the spatial_weights_definition parameter to get the spatial diagnostics. Based on spatial statistics, it suggests the regression algorithm. You have to provide spatial weights definition when using this algorithm, otherwise, the algorithm recommends OLSRegressor.

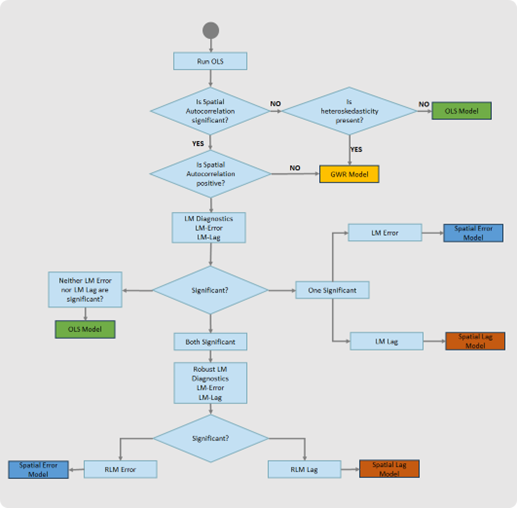
The following figure shows the current workflow for choosing the best algorithm.

From spatial diagnostics, the algorithm gets the Moran's I statistic. If the value is statistically significant, then it is interpreted as follows:

• A positive value of Moran's I statistic indicates the presence of spatial dependence, or spatial clustering, and an algorithm that includes this spatial dependence is preferred. Two algorithms that consider spatial dependence are SpatialLagRegressor and SpatialErrorRegressor. Depending on the Lagrange Multipliers obtained from spatial diagnostics, the algorithm selects one of them (see [3] for more detailed information about spatial regression diagnostics).
• If the Moran's I statistic is negative, then it indicates the presence of regional variance or spatial heteroskedasticity, and a local method such as GWRRegressor is more suitable.

In case the Moran’s I statistic is not statistically significant but the variability of the residuals is significant, then the algorithm selects the GWRRegressor.

See the SpatialAdaptiveRegressor class in Python API Reference for Oracle Spatial AI for more information.

The following example uses the block_groups SpatialDataFrame and SpatialAdaptiveRegressor to train a model from a training set. Then, using a test set, the code estimates the target variable and gets the R-squared metric.

%python

from oraclesai.preprocessing import spatial_train_test_split 
from oraclesai.weights import KNNWeightsDefinition 
from oraclesai.regression import SpatialAdaptiveRegressor 
from oraclesai.pipeline import SpatialPipeline 
from sklearn.preprocessing import StandardScaler 

# Define target and explanatory variables 
X = block_groups[['MEDIAN_INCOME', 'MEAN_AGE', 'MEAN_EDUCATION_LEVEL', 'HOUSE_VALUE', 'INTERNET', 'geometry']] 

# Define training and test sets 
X_train, X_test, _, _, _, _ = spatial_train_test_split(X, y="MEDIAN_INCOME", test_size=0.2, random_state=32) 

# Define spatial weights 
weights_definition = KNNWeightsDefinition(k=5) 

# Create an instance of SpatialAdaptiveRegressor 
spreg_model = SpatialAdaptiveRegressor(spatial_weights_definition=weights_definition)

# Add the model to a spatial pipeline along with a preprocessing step 
spreg_pipeline = SpatialPipeline([('scale', StandardScaler()), ('spreg_regression', spreg_model)]) 

# Train the model 
spreg_pipeline.fit(X_train, "MEDIAN_INCOME") 

# Print the selected model 
print(f">> Algorithm chosen: {spreg_pipeline.named_steps['spreg_regression'].model_type.__name__}") 

# Print the predictions with the test set 
spreg_predictions_test = spreg_pipeline.predict(X_test.drop("MEDIAN_INCOME")).flatten() 
print(f"\n>> predictions (X_test):\n {spreg_predictions_test[:10]}") 

# Print the score with the test set 
spreg_r2_score = spreg_pipeline.score(X_test, "MEDIAN_INCOME") 
print(f"\n>> r2_score (X_test):\n {spreg_r2_score}")

The output of the program consists of the name of the algorithm chosen by SpatialAdaptiveRegressor, the predictions of the first 10 observations of the test set, and the R-squared metric of the test set.

> Algorithm chosen: ErrorModel

>> predictions (X_test):
 [101563.4135695  105231.46019748  24081.18722085  38529.02025428
 164280.78271333  50332.38349005 102590.59769969  27659.63416001
  81911.84382123  17657.93225933]

>> r2_score (X_test):
 0.6456845274014411